题目内容
16.设a≤3,函数f(x)=x|x-a|-a.(1)若f(x)为奇函数,求a的值;
(2)若对任意的x∈[2,3],f(x)≥0恒成立,求a的取值范围.
分析 (1)根据f(0)=0即可求出a;
(2)讨论a的取值:a<2,2≤a≤3,两种情况,求出每种情况下的f(x)的最小值,让最小值大于等于0从而求出a的取值范围.
解答 解:(1)∵f(x)在原点有定义,f(x)为奇函数;
∴f(0)=-a=0;
∴a=0;
(2)f(x)=x|x-a|-a;
∴①若a<2,则x=2时,f(x)在[2,3]上取得最小值f(2)=2(2-a)-a=4-3a;
∴4-3a≥0,a≤$\frac{4}{3}$;
∴a≤$\frac{4}{3}$;
②若2≤a≤3,则x=a时,f(x)取得最小值f(a)=-a;
-a<0,不满足f(x)≥0;
即这种情况不存在.
∴综上得a的取值范围为(-∞,$\frac{4}{3}$].
点评 考查奇函数的定义,奇函数在原点有定义时f(0)=0,函数零点的定义,含绝对值函数求最值的方法,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.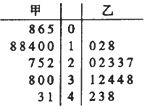 从甲乙两个城市分别随机抽取16台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图所示,设甲乙两组数据的平均数分别为x甲,x乙,中位数分别为m甲,m乙,则( )
从甲乙两个城市分别随机抽取16台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图所示,设甲乙两组数据的平均数分别为x甲,x乙,中位数分别为m甲,m乙,则( )
 从甲乙两个城市分别随机抽取16台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图所示,设甲乙两组数据的平均数分别为x甲,x乙,中位数分别为m甲,m乙,则( )
从甲乙两个城市分别随机抽取16台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图所示,设甲乙两组数据的平均数分别为x甲,x乙,中位数分别为m甲,m乙,则( )| A. | x甲<x乙,m甲>m乙 | B. | x甲<x乙,m甲<m乙 | C. | x甲>x乙,m甲>m乙 | D. | x甲>x乙,m甲<m乙 |
1.下列说法不正确的是( )
| A. | 综合法是由因导果的顺推证法 | |
| B. | 分析法是执果索因的逆推证法 | |
| C. | 分析法是从要证的结论出发,寻求使它成立的充分条件 | |
| D. | 综合法与分析法在同一题的证明中不可能同时采用 |
5.函数f(x)=ax-1+2的图象恒过定点( )
| A. | (3,1) | B. | (0,2) | C. | (1,3) | D. | (0,1) |
 如图,在三棱锥P-ABC中,直线PA⊥平面ABC,且∠ABC=90°,又点Q,M,N分别是线段PB,AB,BC的中点,且点K是线段MN上的动点
如图,在三棱锥P-ABC中,直线PA⊥平面ABC,且∠ABC=90°,又点Q,M,N分别是线段PB,AB,BC的中点,且点K是线段MN上的动点