题目内容
7.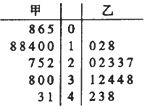 从甲乙两个城市分别随机抽取16台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图所示,设甲乙两组数据的平均数分别为x甲,x乙,中位数分别为m甲,m乙,则( )
从甲乙两个城市分别随机抽取16台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图所示,设甲乙两组数据的平均数分别为x甲,x乙,中位数分别为m甲,m乙,则( )| A. | x甲<x乙,m甲>m乙 | B. | x甲<x乙,m甲<m乙 | C. | x甲>x乙,m甲>m乙 | D. | x甲>x乙,m甲<m乙 |
分析 直接求出甲与乙的平均数,以及甲与乙的中位数,即可得到选项
解答 解:甲的平均数$\overline{x}$甲=$\frac{1}{16}$(5+6+8+10+10+14+18+18+22+25+27+30+30+38+41+43)=$\frac{345}{16}$,
乙的平均数$\overline{x}$乙=$\frac{1}{16}$(10+12+18+20+22+23+23+27+31+32+34+34+38+42+43+48)=$\frac{457}{16}$,
所以$\overline{x}$甲<$\overline{x}$乙.
甲的中位数为20,乙的中位数为29,所以m甲<m乙,
故选:B.
点评 本题考查茎叶图,众数、中位数、平均数的应用,考查计算能力.

练习册系列答案
相关题目
15.下列命题中,真命题的是( )
| A. | 1弧度是一度的圆心角所对的弧 | |
| B. | 1弧度是长度为半径的弧 | |
| C. | 1弧度是一度的弧与一度的角之和 | |
| D. | 1弧度是长度等于半径长的弧所对的圆心角的大小 |
12.如果命题“¬(p∨q)”为假命题,那么( )
| A. | p、q中至少一个有一个为真命题 | B. | p、q均为假命题 | ||
| C. | p、q均为真命题 | D. | p、q中至多一个有一个为真命题 |
19.已知函数y=f(lg(x+1))的定义域为(0,99],则函数y=f[log2(x+2)]的定义域为( )
| A. | (-1,2] | B. | (-1,3) | C. | (-2,1] | D. | (-1,2) |