题目内容
设等差数列{an},已知a5=-3,S10=-40
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{abn}为等比数列,且b1=5,b2=8,求数列{bn}的前n项和Tn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{abn}为等比数列,且b1=5,b2=8,求数列{bn}的前n项和Tn.
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)设等差数列{an}的首项为a1、公差为d,依题意a5=-3,S10=-40,可求得a1=5,d=-2,于是可得数列{an}的通项公式;
(Ⅱ)由题意可求得等比数列{abn}的通项公式abn=(-3)×3n-1=-3n,又abn=7-2bn,于是可得bn=
+
,再分组求和即可.
(Ⅱ)由题意可求得等比数列{abn}的通项公式abn=(-3)×3n-1=-3n,又abn=7-2bn,于是可得bn=
| 7 |
| 2 |
| 3n |
| 2 |
解答:
解:(Ⅰ)设等差数列{an}的首项为a1、公差为d,
∵a5=-3,S10=-40,
∴
解得:a1=5,d=-2.
∴an=7-2n.
(Ⅱ)由(Ⅰ)知,an=7-2n,又数列{abn}为等比数列,且b1=5,b2=8,
∴q=
=
=
=3,
又ab1=a5=7-2×5=-3,
∴abn=(-3)×3n-1=-3n,又abn=7-2bn,
∴7-2bn=-3n,
∴bn=
+
,
∴数列{bn}的前n项和
Tn=b1+b2+…+bn=
+
(3+32+…+3n)
=
+
•
=
+
.
∵a5=-3,S10=-40,
∴
|
解得:a1=5,d=-2.
∴an=7-2n.
(Ⅱ)由(Ⅰ)知,an=7-2n,又数列{abn}为等比数列,且b1=5,b2=8,
∴q=
| ab2 |
| ab1 |
| a8 |
| a5 |
| 7-2×8 |
| 7-2×5 |
又ab1=a5=7-2×5=-3,
∴abn=(-3)×3n-1=-3n,又abn=7-2bn,
∴7-2bn=-3n,
∴bn=
| 7 |
| 2 |
| 3n |
| 2 |
∴数列{bn}的前n项和
Tn=b1+b2+…+bn=
| 7n |
| 2 |
| 1 |
| 2 |
=
| 7n |
| 2 |
| 1 |
| 2 |
| 3(1-3n) |
| 1-3 |
| 7n |
| 2 |
| 3n+1-3 |
| 4 |
点评:本题考查等差数列与等比数列的通项公式的确定,考查等价转化思想与综合应用能力,(Ⅱ)中求得bn=
+
是关键,属于难题.
| 7 |
| 2 |
| 3n |
| 2 |

练习册系列答案
相关题目
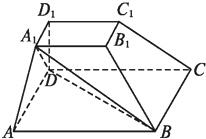 如图,在四棱台ABCD-A1B1C1D1中,D1D⊥平面ABCD,底面ABCD是平行四边形,AB=2A1B1=2AD=2DD1,∠BAD=60°.
如图,在四棱台ABCD-A1B1C1D1中,D1D⊥平面ABCD,底面ABCD是平行四边形,AB=2A1B1=2AD=2DD1,∠BAD=60°. 如图,已知点D、E分别是三棱柱ABC-A1B1C1的棱BC、A1B1的中点.求证:VE-ABD=2VE-DC
如图,已知点D、E分别是三棱柱ABC-A1B1C1的棱BC、A1B1的中点.求证:VE-ABD=2VE-DC