题目内容
已知定义在R上函数f(x)=
为奇函数.
(Ⅰ)求a+b的值;
(Ⅱ)求函数f(x)的值域.
| x+b |
| x2+ax+1 |
(Ⅰ)求a+b的值;
(Ⅱ)求函数f(x)的值域.
考点:函数奇偶性的判断,函数的值域
专题:函数的性质及应用
分析:(Ⅰ)根据函数是奇函数,建立方程关系即可求a+b的值;
(Ⅱ)利用判别式法,将函数转化为一元二次方程,可求函数f(x)的值域.
(Ⅱ)利用判别式法,将函数转化为一元二次方程,可求函数f(x)的值域.
解答:
解:(Ⅰ)由f(x)为R上的奇函数,知f(0)=0,f(-1)=-f(1),
即f(0)=b=0,
=-
,
由此解得a=0,b=0,故a+b=0.
(Ⅱ)f(x)=
,设y=
,则等价为方程yx2-x+y=0有根,
当y=0时,根为x=0符合;
当y≠0时,则△=1-4y2≥0,
于是-
≤y≤
且y≠0;
综上-
≤y≤
,
综上,值域为[-
,
].
即f(0)=b=0,
| -1 |
| 1-a+1 |
| 1 |
| 1+a+1 |
由此解得a=0,b=0,故a+b=0.
(Ⅱ)f(x)=
| x |
| x2+1 |
| x |
| x2+1 |
当y=0时,根为x=0符合;
当y≠0时,则△=1-4y2≥0,
于是-
| 1 |
| 2 |
| 1 |
| 2 |
综上-
| 1 |
| 2 |
| 1 |
| 2 |
综上,值域为[-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查函数奇偶性的应用,以及函数值域的求解,利用判别式法是解决本题的关键和技巧.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
过点M(2,1)且在坐标轴上的截距相等的直线共有( )
| A、1条 | B、2条 | C、3条 | D、4条 |
对于命题p:若|
|=|
|=2,
与
的夹角是
,则向量
在
方向上的投影是1;命题q:“x≤1”是“
≥1”的必要不充分条件,下列判断正确的是( )
| a |
| b |
| a |
| b |
| 2π |
| 3 |
| b |
| a |
| 1 |
| x |
| A、¬q为假命题 |
| B、¬p为假命题 |
| C、“p∧q”是真命题 |
| D、“p∨q”是假命题 |
两位工人加工同一种零件共100个,甲加工了40个,其中35个是合格品,乙加工了60个,其中有50个合格,令A事件为”从100个产品中任意取一个,取出的是合格品”,B事件为”从100个产品中任意取一个,取到甲生产的产品”,则P(A|B)等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=loga(2x+b-1)(a>0且a≠1)的部分图象如图所示,则满足a,b关系是( )
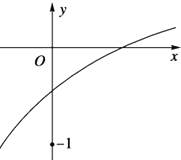

A、0<
| ||||
B、0<b<
| ||||
C、0<
| ||||
D、0<
|