题目内容
在△ABC中,若a=4,b=3,cosA=
,则B=( )
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:正弦定理
专题:计算题,三角函数的求值
分析:先利用同角三角函数关系求得sinA的值,进而利用正弦定理求得sinB的值,最后求得B.
解答:
解:∵cosA=
,0<∠A<π
∴sinA=
=
=
∵
=
,即
=
,
∴sinB=
,
∴∠B=
或
,
∵sinA=
>
∴∠A>
∴∠B=
与三角形内角和为180°矛盾.
∴∠B=
,
故选A.
| 1 |
| 3 |
∴sinA=
| 1-cos2A |
1-
|
2
| ||
| 3 |
∵
| a |
| sinA |
| b |
| sinB |
| 4 | ||||
|
| 3 |
| sinB |
∴sinB=
| ||
| 2 |
∴∠B=
| π |
| 4 |
| 3π |
| 4 |
∵sinA=
2
| ||
| 3 |
| ||
| 2 |
∴∠A>
| π |
| 4 |
∴∠B=
| 3π |
| 4 |
∴∠B=
| π |
| 4 |
故选A.
点评:本题主要考查了正弦定理的应用.解题的过程中注意对结果正负号的判断.

练习册系列答案
相关题目
若
,
不同为零向量,则条件“存在实数λ,使得
=λ
”是“
∥
”的( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
设集合M={x|2x<
},N={x|-2≤x≤3},则M∩N=( )
| 1 |
| 2 |
| A、[-2,1) |
| B、[-2,-l) |
| C、(-1,3] |
| D、[-2,3] |
若Sn=cos
+cos
+…+cos
(n∈N*),则在S1,S2,…,S2014中,正数的个数是( )
| π |
| 8 |
| 2π |
| 8 |
| nπ |
| 8 |
| A、882 | B、756 |
| C、750 | D、378 |
如果
+
=1表示焦点在x轴上的椭圆,则实数a的取值范围为( )
| x2 |
| a2 |
| y2 |
| a+2 |
| A、(-2,+∞) |
| B、(-2,-1)∪(2,+∞) |
| C、(-∞,-1)∪(2,+∞) |
| D、任意实数R |
直线3x-y+1=0的斜率是( )
| A、3 | ||
| B、-3 | ||
C、
| ||
D、-
|
已知一几何体三视图如图,则其体积为( )
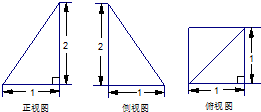

A、
| ||
B、
| ||
| C、1 | ||
| D、2 |