ĢāÄæÄŚČŻ
ŅŃÖŖ¶ØµćF1£Ø-
£¬0£©£¬F2£Ø
£¬0£©£¬¶ÆµćRŌŚĒśĻßCÉĻŌĖ¶ÆĒŅ±£³Ö|RF1|+|RF2|µÄÖµ²»±ä£¬ĒśĻßC¹żµćT£Ø0£¬1£©£¬
£Ø¢ń£©ĒóĒśĻßCµÄ·½³Ģ£»
£Ø¢ņ£©MŹĒĒśĻßCÉĻŅ»µć£¬¹żµćM×÷Š±ĀŹ·Ö±šĪŖk1ŗĶk2µÄÖ±ĻßMA£¬MB½»ĒśĻßCÓŚA”¢BĮ½µć£¬ČōA”¢B¹ŲÓŚŌµć¶Ō³Ę£¬Ēók1•k2µÄÖµ£»
£Ø¢ó£©Ö±Ļßl¹żµćF2£¬ĒŅÓėĒśĻßC½»ÓŚPQ£¬ÓŠČēĻĀĆüĢāp£ŗ”°µ±Ö±Ļßl“¹Ö±ÓŚxÖįŹ±£¬”÷F1PQµÄĆ껿ȔµĆ×ī“óÖµ”±£®ÅŠ¶ĻĆüĢāpµÄÕę¼Ł£®ČōŹĒÕęĆüĢā£¬ĒėøųÓčÖ¤Ć÷£»ČōŹĒ¼ŁĆüĢā£¬ĒėĖµĆ÷ĄķÓÉ£®
| 3 |
| 3 |
£Ø¢ń£©ĒóĒśĻßCµÄ·½³Ģ£»
£Ø¢ņ£©MŹĒĒśĻßCÉĻŅ»µć£¬¹żµćM×÷Š±ĀŹ·Ö±šĪŖk1ŗĶk2µÄÖ±ĻßMA£¬MB½»ĒśĻßCÓŚA”¢BĮ½µć£¬ČōA”¢B¹ŲÓŚŌµć¶Ō³Ę£¬Ēók1•k2µÄÖµ£»
£Ø¢ó£©Ö±Ļßl¹żµćF2£¬ĒŅÓėĒśĻßC½»ÓŚPQ£¬ÓŠČēĻĀĆüĢāp£ŗ”°µ±Ö±Ļßl“¹Ö±ÓŚxÖįŹ±£¬”÷F1PQµÄĆ껿ȔµĆ×ī“óÖµ”±£®ÅŠ¶ĻĆüĢāpµÄÕę¼Ł£®ČōŹĒÕęĆüĢā£¬ĒėøųÓčÖ¤Ć÷£»ČōŹĒ¼ŁĆüĢā£¬ĒėĖµĆ÷ĄķÓÉ£®
æ¼µć£ŗÖ±ĻßÓėŌ²×¶ĒśĻߵĹŲĻµ,ĆüĢāµÄÕę¼ŁÅŠ¶ĻÓėÓ¦ÓĆ,¹ģ¼£·½³Ģ
×ØĢā£ŗŌ²×¶ĒśĻߵĶØŅ唢ŠŌÖŹÓė·½³Ģ
·ÖĪö£ŗ£Ø¢ń£©ÓÉĢāŅāĒóµĆ|RF1|+|RF2|=4£¬·ūŗĻĶÖŌ²¶ØŅ壬ĒŅĒóµĆa£¬cµÄÖµ£¬½ųŅ»²½µĆµ½b2µÄÖµ£¬ŌņĒśĻßCµÄ·½³ĢæÉĒó£»
£Ø¢ņ£©ÉčM£Øx0£¬y0£©£¬A£Øx1£¬y1£©£¬B£Ø-x1£¬-y1£©£¬ÓɵćM£¬AŌŚĶÖŌ²ÉĻµĆµ½M£¬AµÄ×ų±źµÄĮ½øö·½³Ģ£¬×÷²īŗóµĆµ½
+y02-y12=0£¬ÓÉĮ½µćŹ½µĆµ½k1ŗĶk2£¬½įŗĻÉĻŹ½¼“æÉĒóµĆk1•k2=
=-
£»
£Ø¢ó£©ÉčÖ±ĻßlµÄ·½³ĢĪŖx=my+
£¬“śČėĶÖŌ²·½³Ģ
+y2=1£¬ÓÉĻŅ³¤¹«Ź½°Ń|PQ|ÓĆŗ¬ÓŠmµÄ“śŹżŹ½±ķŹ¾£¬Ēó³öF1µ½Ö±ĻßlµÄ¾ąĄė£¬“śČė£¬”÷F1PQµÄĆ껿¹«Ź½£¬»»ŌŖŗóĄūÓĆ»ł±¾²»µČŹ½Ēó×īÖµ£®Ēó³ö”÷F1PQµÄĆ껿ȔµĆ×ī“óÖµŹ±µÄmÖµ£¬“Ó¶ųµĆµ½Ö±Ļß·½³Ģ£¬ĖµĆ÷ĆüĢāpŹĒ¼ŁĆüĢā£®
£Ø¢ņ£©ÉčM£Øx0£¬y0£©£¬A£Øx1£¬y1£©£¬B£Ø-x1£¬-y1£©£¬ÓɵćM£¬AŌŚĶÖŌ²ÉĻµĆµ½M£¬AµÄ×ų±źµÄĮ½øö·½³Ģ£¬×÷²īŗóµĆµ½
| x02-x12 |
| 4 |
| y02-y12 |
| x02-x12 |
| 1 |
| 4 |
£Ø¢ó£©ÉčÖ±ĻßlµÄ·½³ĢĪŖx=my+
| 3 |
| x2 |
| 4 |
½ā“š£ŗ
½ā£ŗ£Ø¢ń£©”ß|RF1|+|RF2|=|TF1|+|TF2|=2
=4£¾|F1F2|=2
£¬
”ąĒśĻßCĪŖŅŌŌµćĪŖÖŠŠÄ£¬F1”¢F2ĪŖ½¹µćµÄĶÖŌ²£¬
ÉčĘä°ė³¤ÖįĪŖa£¬°ė¶ĢÖįĪŖb£¬°ė½¹¾ąĪŖc£¬Ōņ2a=2£¬2c=2
£¬
”ąa=2£¬c=
£¬b2=a2-c2=1£®
”ąĒśĻßCµÄ·½³ĢĪŖ
+y2=1£»
£Ø¢ņ£©ÉčM£Øx0£¬y0£©£¬A£Øx1£¬y1£©ŌņB£Ø-x1£¬-y1£©£¬
”ßµćM£¬AŌŚĶÖŌ²
+y2=1ÉĻ£¬
”ą
+y02=1£¬
+y12=1£¬
Ļą¼õµĆ
+y02-y12=0£¬
ÓÖk1=
£¬k2=
£¬
”ąk1•k2=
=-
£»
£Ø¢ó£©ÉčÖ±ĻßlµÄ·½³ĢĪŖx=my+
£¬“śČėĶÖŌ²·½³Ģ
+y2=1£¬
µĆ(4+m2)y2+2
my-1=0£¬¼ĘĖć²¢ÅŠ¶ĻµĆ”÷£¾0£¬
ÉčP£Øx3£¬y3£©£¬Q£Øx4£¬y4£©£¬µĆ
£¬
”ą|PQ|=
=
=
£®
F1µ½Ö±ĻßlµÄ¾ąĄėd=
£¬
Éčt=
£¬Ōņt”Ż1£¬
”ąS”÷F1PQ=
|PQ|•d=4
”Į
=
=
”Ü2£®
µ±t2=3£¬¼“m2=2£¬m=”Ą
Ź±£¬”÷F1PQµÄĆ껿×ī“ó£®
”ąŌĆüĢāŹĒ¼ŁĆüĢā£¬”÷F1PQµÄĆ껿ȔµĆ×ī“óÖµŹ±£¬Ö±ĻßlµÄ·½³ĢĪŖ£ŗ
x+
y-
=0ŗĶx-
y-
=0£®
(
|
| 3 |
”ąĒśĻßCĪŖŅŌŌµćĪŖÖŠŠÄ£¬F1”¢F2ĪŖ½¹µćµÄĶÖŌ²£¬
ÉčĘä°ė³¤ÖįĪŖa£¬°ė¶ĢÖįĪŖb£¬°ė½¹¾ąĪŖc£¬Ōņ2a=2£¬2c=2
| 3 |
”ąa=2£¬c=
| 3 |
”ąĒśĻßCµÄ·½³ĢĪŖ
| x2 |
| 4 |
£Ø¢ņ£©ÉčM£Øx0£¬y0£©£¬A£Øx1£¬y1£©ŌņB£Ø-x1£¬-y1£©£¬
”ßµćM£¬AŌŚĶÖŌ²
| x2 |
| 4 |
”ą
| x02 |
| 4 |
| x12 |
| 4 |
Ļą¼õµĆ
| x02-x12 |
| 4 |
ÓÖk1=
| y0-y1 |
| x0-x1 |
| y0+y1 |
| x0+x1 |
”ąk1•k2=
| y02-y12 |
| x02-x12 |
| 1 |
| 4 |
£Ø¢ó£©ÉčÖ±ĻßlµÄ·½³ĢĪŖx=my+
| 3 |
| x2 |
| 4 |
µĆ(4+m2)y2+2
| 3 |
ÉčP£Øx3£¬y3£©£¬Q£Øx4£¬y4£©£¬µĆ
|
”ą|PQ|=
| (x3-x4)2+(y3-y4)2 |
| (1+m2)[(y3+y4)2-4y3y4] |
=
| 4(1+m2) |
| 4+m2 |
F1µ½Ö±ĻßlµÄ¾ąĄėd=
2
| ||
|
Éčt=
| 1+m2 |
”ąS”÷F1PQ=
| 1 |
| 2 |
| 3 |
| ||
| 4+m2 |
=
4
| ||
| t2+3 |
4
| ||
t+
|
µ±t2=3£¬¼“m2=2£¬m=”Ą
| 2 |
”ąŌĆüĢāŹĒ¼ŁĆüĢā£¬”÷F1PQµÄĆ껿ȔµĆ×ī“óÖµŹ±£¬Ö±ĻßlµÄ·½³ĢĪŖ£ŗ
x+
| 2 |
| 3 |
| 2 |
| 3 |
µćĘĄ£ŗ±¾Ģāæ¼²éĮĖ¹ģ¼£·½³Ģ£¬æ¼²éĮĖÖ±ĻßÓėŌ²×¶ĒśĻߵĹŲĻµ£¬ŃµĮ·ĮĖ”°µć²ī·Ø”±£¬æ¼²éĮĖĻŅ³¤¹«Ź½µÄÓ¦ÓĆ£¬ŃµĮ·ĮĖĄūÓĆ»ł±¾²»µČŹ½Ēó×īÖµ£¬Éę¼°Ö±ĻßÓėŌ²×¶ĒśĻߵĹŲĻµĪŹĢā£¬³£°ŃÖ±ĻßÓėŌ²×¶ĒśĻßĮŖĮ¢£¬»ÆĪŖ¹ŲÓŚxµÄŅ»ŌŖ¶ž“Ī·½³ĢŗóĄūÓĆøłÓėĻµŹż¹ŲĻµĒó½ā£®“ĖĢāŹĒøßæ¼ŹŌ¾ķÖŠµÄŃ¹ÖįĢā£®

Į·Ļ°²įĻµĮŠ“š°ø
Ļą¹ŲĢāÄæ
ŌŚ³¤ĪŖ8µÄĻ߶ĪABÉĻČĪČ”Ņ»µćC£¬ĻÖ×÷Ņ»¾ŲŠĪ£¬ĮŚ±ß³¤·Ö±šµČÓŚAC”¢BCµÄ³¤£¬ŌņøĆ¾ŲŠĪĆ껿“óÓŚ15µÄøÅĀŹ£Ø””””£©
AӢ
| ||
BӢ
| ||
CӢ
| ||
DӢ
|
µ±ŹµŹżx£¬yĀś×ć²»µČŹ½
Ź±£¬ŗćÓŠax+y”Ü2³ÉĮ¢£¬ŌņŹµŹżaµÄȔֵ¼ÆŗĻŹĒ£Ø””””£©
|
| A”¢£Ø0£¬1] |
| B”¢£Ø-”Ž£¬1] |
| C”¢£Ø-1£¬1] |
| D”¢£Ø1£¬2£© |
ČēĶ¼øų³öµÄŹĒ¼ĘĖć1+
+
+”+
µÄÖµµÄŅ»øö³ĢŠņæņĶ¼£¬ĘäÖŠÅŠ¶ĻæņÄŚÓ¦ĢīČėµÄĢõ¼žŹĒ£Ø””””£©

| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 11 |

| A”¢i£¼12 | B”¢i£¾11 |
| C”¢i£¼11 | D”¢i”Ü6 |
 ČēĶ¼1£¬”÷ABCĪŖÕżČż½ĒŠĪ£¬”÷BCDĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬”ĻBCD=90”ć£¬½«”÷ABCŃŲBC±ßÕŪµžµ½”÷A”äBCµÄĪ»ÖĆ£¬Ź¹A”äB=A”äD£¬EĪŖBDÖŠµć£¬ČēĶ¼2£®
ČēĶ¼1£¬”÷ABCĪŖÕżČż½ĒŠĪ£¬”÷BCDĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬”ĻBCD=90”ć£¬½«”÷ABCŃŲBC±ßÕŪµžµ½”÷A”äBCµÄĪ»ÖĆ£¬Ź¹A”äB=A”äD£¬EĪŖBDÖŠµć£¬ČēĶ¼2£®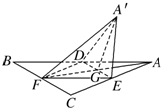 ČēĶ¼£¬ÕżČż½ĒŠĪABCµÄÖŠĻßAFÓėÖŠĪ»ĻßDEĻą½»ÓŚµćG£¬ŅŃÖŖ”÷A”äEDŹĒ”÷AEDČĘDEŠż×Ŗ¹ż³ĢÖŠµÄŅ»øöĶ¼ŠĪ£¬ĻÖøų³öĻĀĮŠĖÄøöĆüĢā£ŗ
ČēĶ¼£¬ÕżČż½ĒŠĪABCµÄÖŠĻßAFÓėÖŠĪ»ĻßDEĻą½»ÓŚµćG£¬ŅŃÖŖ”÷A”äEDŹĒ”÷AEDČĘDEŠż×Ŗ¹ż³ĢÖŠµÄŅ»øöĶ¼ŠĪ£¬ĻÖøų³öĻĀĮŠĖÄøöĆüĢā£ŗ