题目内容
15.函数$f(x)=\sqrt{x+1}$的定义域为( )| A. | (5,+∞) | B. | [-1,5)∪(5,+∞) | C. | [-1,5) | D. | [-1,+∞) |
分析 根据二次根式的性质求出函数的定义域即可.
解答 解:由题意得:x+1≥0,
解得:x≥-1,
故函数的定义域是[-1,+∞),
故选:D.
点评 本题考查了二次根式的性质,考查函数的定义域问题,是一道基础题.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
5.下列说法正确的是( )
| A. | 命题“2≥1”是假命题 | |
| B. | 命题“?x∈R,x2+1>0”的否定是:$?{x_0}∈R,{x_0}^2+1$<0 | |
| C. | 命题“若2a>2b,则a>b”的否命题是“若2a>2b,则a≤b” | |
| D. | “x>1”是“x2+x+2>0”充分不必要条件 |
6.已知直线l的方向向量为$\vec s=(1,2,x)$,平面α的法向量$\vec n=(-2,y,2)$,若l?α,则xy的最大值为( )
| A. | 1 | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{8}$ |
10.近年来我国电子商务行业迎来发展的新机遇.2016年双11期间,某购物平台的销售业绩高达918亿人民币.与此同时,相关管理部门推出了针对电商的商品和服务的评价体系.现从评价系统中选出200次成功交易,并对其评价进行统计,对商品的好评率为0.6,对服务的好评率为0.75,其中对商品和服务都作出好评的交易为80次.
(1)能否在犯错误的概率不超过0.001的前提下,认为商品好评与服务好评有关?
(2)若将频率视作概率,某人在该购物平台上进行5次购物中,设对商品和服务全好评的次数为随机变量X:
①求对商品和服务全为好评的次数X的分布列(概率用组合数算式表示);
②求X的数学期望和方程.
(K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
(1)能否在犯错误的概率不超过0.001的前提下,认为商品好评与服务好评有关?
(2)若将频率视作概率,某人在该购物平台上进行5次购物中,设对商品和服务全好评的次数为随机变量X:
①求对商品和服务全为好评的次数X的分布列(概率用组合数算式表示);
②求X的数学期望和方程.
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
20.等比数列{an}的前n项和为Sn,若a2+S3=0,则公比q=( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
7.已知某几何体的三视图如图所示,则其体积为( )
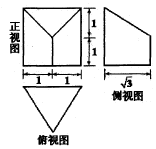

| A. | $2\sqrt{3}$ | B. | $\frac{{5\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
5.设$a={3^{\frac{1}{3}}},b={(\frac{1}{4})^{3.1}},c={log_{0.4}}3$,则a,b,c的大小关系为( )
| A. | c<a<b | B. | c<b<a | C. | b<a<c | D. | a<b<c |