题目内容
5.下列说法正确的是( )| A. | 命题“2≥1”是假命题 | |
| B. | 命题“?x∈R,x2+1>0”的否定是:$?{x_0}∈R,{x_0}^2+1$<0 | |
| C. | 命题“若2a>2b,则a>b”的否命题是“若2a>2b,则a≤b” | |
| D. | “x>1”是“x2+x+2>0”充分不必要条件 |
分析 利用命题的定义以及四个命题之间的关系分别对选项分析选择.
解答 解:A,“2≥1”不是命题;故A错误;
B.命题“?x∈R,x2+1>0”的否定是:$?{x_0}∈R,{x_0}^2+1$≥0;故B错误;
C.命题“若2a>2b,则a>b”的否命题是“若2a≤2b,则a≤b”;故C错误;
D.“x>1”能够推出“x2+x+2>0”;但是“x2+x+2>0”⇒x∈R,不一定⇒“x>1”;所以“x>1”是充分不必要条件.
故选:D.
点评 本题以命题的真假判断与应用为载体,考查了四种命题,充要条件,特称命题的否定等知识点,属于基础题.

练习册系列答案
相关题目
16.以下四个命题中,真命题是( )
| A. | ?x∈(0,π),sinx=tanx | |
| B. | “?x∈R,x2+x+1>0”的否定是“?x0∈R,x02+x0+1<0” | |
| C. | ?θ∈R,函数f(x)=sin(2x+θ)都不是偶函数 | |
| D. | 条件p:$\left\{\begin{array}{l}{x+y>4}\\{xy>4}\end{array}\right.$,条件q:$\left\{\begin{array}{l}{x>2}\\{y>2}\end{array}\right.$则p是q的必要不充分条件 |
13.双曲线实半轴长为2,焦点为(-3,0)、(3,0),则该双曲线为( )
| A. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{9}$=1 | B. | $\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1 | D. | $\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{5}$=1 |
14.执行如图所示的程序框图,则输出S=( )
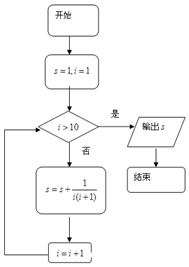

| A. | $\frac{5}{11}$ | B. | $\frac{21}{11}$ | C. | $\frac{13}{9}$ | D. | $\frac{17}{9}$ |
15.函数$f(x)=\sqrt{x+1}$的定义域为( )
| A. | (5,+∞) | B. | [-1,5)∪(5,+∞) | C. | [-1,5) | D. | [-1,+∞) |
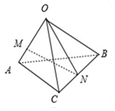 如图,空间四边形OACB中,$\overrightarrow{{O}{A}}$=$\overrightarrow{a}$,$\overrightarrow{{O}{B}}$=$\overrightarrow{b}$,$\overrightarrow{{O}C}$=$\overrightarrow{c}$,点M在OA上,且$\overrightarrow{OM}=\frac{2}{3}\overrightarrow{OA}$,点N为BC中点,则$\overrightarrow{MN}$等于$-\frac{2}{3}\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}+\frac{1}{2}\overrightarrow{c}$.(用向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示)
如图,空间四边形OACB中,$\overrightarrow{{O}{A}}$=$\overrightarrow{a}$,$\overrightarrow{{O}{B}}$=$\overrightarrow{b}$,$\overrightarrow{{O}C}$=$\overrightarrow{c}$,点M在OA上,且$\overrightarrow{OM}=\frac{2}{3}\overrightarrow{OA}$,点N为BC中点,则$\overrightarrow{MN}$等于$-\frac{2}{3}\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}+\frac{1}{2}\overrightarrow{c}$.(用向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示)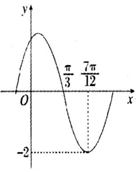 函数$f(x)=Asin({ωx+φ})({A>0,ω>0,|φ|≤\frac{π}{2}})$的部分图象如图所示,其中$f({\frac{π}{3}})=0,f({\frac{7π}{12}})=-2$,给出下列结论:
函数$f(x)=Asin({ωx+φ})({A>0,ω>0,|φ|≤\frac{π}{2}})$的部分图象如图所示,其中$f({\frac{π}{3}})=0,f({\frac{7π}{12}})=-2$,给出下列结论: