题目内容
6.已知直线l的方向向量为$\vec s=(1,2,x)$,平面α的法向量$\vec n=(-2,y,2)$,若l?α,则xy的最大值为( )| A. | 1 | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{8}$ |
分析 由题意可得:$\overrightarrow{s}⊥\overrightarrow{n}$,因此$\overrightarrow{s}•\overrightarrow{n}$=0,可得 x+y=1.再利用基本不等式的性质即可得出.
解答 解:由题意可得:$\overrightarrow{s}⊥\overrightarrow{n}$,
∴$\overrightarrow{s}•\overrightarrow{n}$=-2+2y+2x=0,可得 x+y=1.
取x,y>0,则$1≥2\sqrt{xy}$,可得xy$≤\frac{1}{4}$,当且仅当x=y=$\frac{1}{2}$时取等号.
故选:B.
点评 本题考查了空间向量垂直与数量积的关系、基本不等式的性质、线面垂直的性质定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
14.执行如图所示的程序框图,则输出S=( )
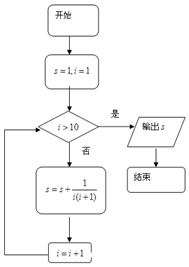

| A. | $\frac{5}{11}$ | B. | $\frac{21}{11}$ | C. | $\frac{13}{9}$ | D. | $\frac{17}{9}$ |
18.设全集U={0,1,2,3,4},集合A={0,1,3},集合B={2,3},则∁U(A∪B)=( )
| A. | {4} | B. | {0,1,2,3} | C. | {3} | D. | {0,1,2,4} |
15.函数$f(x)=\sqrt{x+1}$的定义域为( )
| A. | (5,+∞) | B. | [-1,5)∪(5,+∞) | C. | [-1,5) | D. | [-1,+∞) |