题目内容
3.设P,Q分别是圆x2+(y-1)2=3和椭圆$\frac{x^2}{4}+{y^2}=1$上的点,则P,Q两点间的最大距离是$\frac{7\sqrt{3}}{3}$.分析 圆心C(0,1)到椭圆上的点Q(2cosα,sinα)(α∈[0,2π))的距离d=$\sqrt{(2cosα)^{2}+(sinα-1)^{2}}$=$\sqrt{\frac{16}{3}-3(sinα+\frac{1}{3})^{2}}$,可得P,Q两点间的最大距离是dmax+r.
解答 解:圆心C(0,1)到椭圆上的点Q(2cosα,sinα)(α∈[0,2π))的距离d=$\sqrt{(2cosα)^{2}+(sinα-1)^{2}}$=$\sqrt{\frac{16}{3}-3(sinα+\frac{1}{3})^{2}}$≤$\frac{4\sqrt{3}}{3}$,当且仅当$sinα=-\frac{1}{3}$时取等号.
∴P,Q两点间的最大距离是d+r=$\frac{4\sqrt{3}}{3}$+$\sqrt{3}$=$\frac{7\sqrt{3}}{3}$.
故答案为:$\frac{7\sqrt{3}}{3}$.
点评 本题考查了椭圆的标准方程及其性质、两点之间的距离公式、三角函数的单调性与值域,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
13.双曲线实半轴长为2,焦点为(-3,0)、(3,0),则该双曲线为( )
| A. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{9}$=1 | B. | $\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1 | D. | $\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{5}$=1 |
14.执行如图所示的程序框图,则输出S=( )
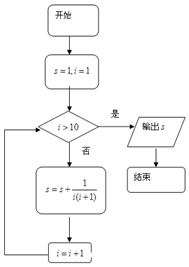

| A. | $\frac{5}{11}$ | B. | $\frac{21}{11}$ | C. | $\frac{13}{9}$ | D. | $\frac{17}{9}$ |
18.设全集U={0,1,2,3,4},集合A={0,1,3},集合B={2,3},则∁U(A∪B)=( )
| A. | {4} | B. | {0,1,2,3} | C. | {3} | D. | {0,1,2,4} |
8.若等边△ABC的边长为3,平面内一点M满足$\overrightarrow{CM}=\frac{1}{3}\overrightarrow{CB}+\frac{1}{2}\overrightarrow{CA}$,则$\overrightarrow{AM}•\overrightarrow{MB}$的值为( )
| A. | 2 | B. | $-\frac{15}{2}$ | C. | $\frac{15}{2}$ | D. | -2 |
15.函数$f(x)=\sqrt{x+1}$的定义域为( )
| A. | (5,+∞) | B. | [-1,5)∪(5,+∞) | C. | [-1,5) | D. | [-1,+∞) |
12.已知集合M={x|-3<x<1},N={-3,-2,-1,0,1},则M∩N等于( )
| A. | {-2,-1,0,1} | B. | {-3,-2,-1,0} | C. | {-2,-1,0} | D. | {-3,-2,-1} |