题目内容
20.等比数列{an}的前n项和为Sn,若a2+S3=0,则公比q=( )| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
分析 利用等比数列的通项公式、求和公式即可得出.
解答 解:∵等比数列{an}满足,a2+S3=0,则a1(1+2q+q2)=0,
即(1+q)2=0,解得q=-1.
故选:A.
点评 本题考查了等比数列的通项公式、数列求和,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
8.若等边△ABC的边长为3,平面内一点M满足$\overrightarrow{CM}=\frac{1}{3}\overrightarrow{CB}+\frac{1}{2}\overrightarrow{CA}$,则$\overrightarrow{AM}•\overrightarrow{MB}$的值为( )
| A. | 2 | B. | $-\frac{15}{2}$ | C. | $\frac{15}{2}$ | D. | -2 |
15.函数$f(x)=\sqrt{x+1}$的定义域为( )
| A. | (5,+∞) | B. | [-1,5)∪(5,+∞) | C. | [-1,5) | D. | [-1,+∞) |
12.已知集合M={x|-3<x<1},N={-3,-2,-1,0,1},则M∩N等于( )
| A. | {-2,-1,0,1} | B. | {-3,-2,-1,0} | C. | {-2,-1,0} | D. | {-3,-2,-1} |
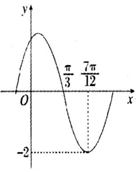 函数$f(x)=Asin({ωx+φ})({A>0,ω>0,|φ|≤\frac{π}{2}})$的部分图象如图所示,其中$f({\frac{π}{3}})=0,f({\frac{7π}{12}})=-2$,给出下列结论:
函数$f(x)=Asin({ωx+φ})({A>0,ω>0,|φ|≤\frac{π}{2}})$的部分图象如图所示,其中$f({\frac{π}{3}})=0,f({\frac{7π}{12}})=-2$,给出下列结论: