题目内容
已知命题p：方程x2+mx+1=0有两个不相等的实根；不等式x2+（m-2）x+1＞0的解集为R；若p或q为真，p且q为假，求实数m的取值范围．
考点：复合命题的真假
专题：
分析：利用一元二次方程有两个不相等的实根与判别式的关系即可得出p，再利用不等式x2+（m-2）x+1＞0的解集为R与判别式的关系即可得出q；由p或q为真，p且q为假，可得p与q为一真一假，进而得出答案．
解答：
解：∵方程x2+mx+1=0有两个不相等的实根，
∴△1=m2-4＞0，∴m＞2或m＜-2
又∵不等式x2+（m-2）x+1＞0的解集为R，
∴△2=16（m-2）2-16＜0，∴0＜m＜4，
∵p或q为真，p且q为假，
∴p与q为一真一假，
（1）当p为真q为假时，
，解得m＜-2或m≥4．
（2）当p为假q为真时，
，解得：0＜m≤2，
综上所述得：m的取值范围是m＜-2或m≥4或0＜m≤2．
∴△1=m2-4＞0，∴m＞2或m＜-2
又∵不等式x2+（m-2）x+1＞0的解集为R，
∴△2=16（m-2）2-16＜0，∴0＜m＜4，
∵p或q为真，p且q为假，
∴p与q为一真一假，
（1）当p为真q为假时，
|
（2）当p为假q为真时，
|
综上所述得：m的取值范围是m＜-2或m≥4或0＜m≤2．
点评：熟练掌握“三个二次”与判别式的关系及其“或”“且”命题的真假的判定是解题的关键．
练习册系列答案
相关题目
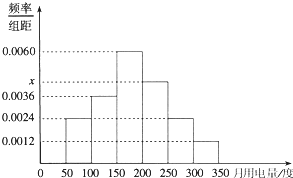从某小区抽取100户居民进行月用电量调查，发现其用电量都在50到350度之间，频率分布直方图如图所示．求
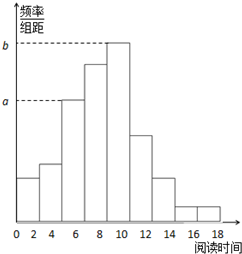从某校随机抽取100名学生，获得了他们一周课外阅读时间（单位：小时）的数据，整理得到数据分组及频数分布表和频率分布直方图：
已知△ABC中，A（2，-1），B（4，3），C（3，-2），求：若函数f（x）在[14，20]上连续，且同时满足f（14）•f（20）＜0，f（14）•f（17）＞0，则（ ）
| A、f（x）在[14，17]上有零点 |
| B、f（x）在[17，20]上有零点 |
| C、f（x）在[14，17]上无零点 |
| D、f（x）在[17，20]上无零点 |