题目内容
求证：sin2αtan2α=tan2α-sin2α
考点：三角函数恒等式的证明,同角三角函数基本关系的运用
专题：证明题,三角函数的求值
分析：由左向右证，先把左边的切函数化成弦函数，然后利用平方关系式把分子中的一个sin2α化成1-cos2α，再整理就可得到右边．
解答：
证明：左边=sin2α
=
=
=tan2α-sin2α=右边
∴sin2αtan2α=tan2α-sin2α．
| sin2α |
| cos2α |
| sin2α(1-cos2α) |
| cos2α |
=
| sin2α-sin2αcos2α |
| cos2α |
∴sin2αtan2α=tan2α-sin2α．
点评：本题考查了三角恒等式的证明，对于三角恒等式的证明，证明的方向有从左向右证，从右向左证，从两边向中间证，有时也可变形证明．证明时要注意分析角的关系和三角函数名称的转化．
练习册系列答案
相关题目
如图，平行四边形ABCD中，AE：EB=m：n，若△AEF的面积等于a，则△CDF的面积等于（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
下列语句能使变量a的值为4的是（ ）
| A、INPUT a=4 |
| B、b=4，b=a |
| C、a=3，a=a+1 |
| D、2a=a+4 |
已知函数f（x）=x2+2bx的图象在点A（0，f（0））处的切线l与直线x-y+3=0平行，若数列{
}的前n项和为Sn，则S2011的值为（ ）
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|
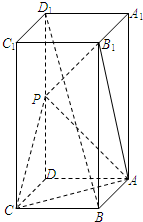如图，在正四棱柱ABCD-A1B1C1D1中，已知AA1=2AB，且点P为DD1的中点．