题目内容
已知函数f(x)=ax2-4ln(x-1),a∈R.
(1)当a=1时,求f(x)的单调区间;
(2)已知点P(1,1)和函数f(x)图象上动点M(m,f(m)),对任意m∈[2,e+1],直线PM倾斜角都是钝角,求a的取值范围.
(1)当a=1时,求f(x)的单调区间;
(2)已知点P(1,1)和函数f(x)图象上动点M(m,f(m)),对任意m∈[2,e+1],直线PM倾斜角都是钝角,求a的取值范围.
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)先求导,再令导数等于0,解导数大于0得函数的增区间,解导数小于0得函数的减区间.(2)可将问题转化为在[2,c+1]上f(x)<1恒成立问题,即在[2,c+1]上f(x)max<1.先求导f′(x)=2ax-
=
,因为x∈[2,c+1],故可只讨论分子的正负问题,不妨令g(x)=ax2-ax-2,讨论g(x)在区间[2,c+1]上的正负问题,同时注意对a的讨论.根据导数正得增区间导数负得减区间,再根据函数的单调性求函数的最值.
| 4 |
| x-1 |
| 2(ax2-ax-2) |
| x-1 |
解答:
解:(1)当a=1时,f(x)=x2-4ln(x-1),x∈(1,+∞),
∴f(x)=2x-
=
=
,
令f′(x)=0,解得:x=2,
∴a=1时,f(x)的单调递增区间为(2,+∞),单调递减区间为(1,2).
(2)∵对任意m∈[2,e+1],直线PM的倾斜角都是钝角,
∴对任意m∈[2,e+1],直线PM的斜率小于0,
即
<0,f(m)<1,
即f(x)在区间[2,e+1]上的最大值小于1,
f(x)=
,x∈(1,+∞),
令g(x)=aa2-ax-2
①当a=0时,f(x)=-4ln(x-1)在[2,e+1]上单调递减,
f(x)max=f(2)=0<1,显然成立,
∴a=0.
②当a<0时,二次函数g(x)的图象开口向下,
且g(0)=-2,g(1)=-2,
?x∈(1,+∞),g(x)<0,
故f′(x)<0,f(x)在(1,+∞)上单调递减,
故f(x)在[2,e+1]上单调递减,f(x)max=f(2)=4a<0,显然成立,
∴a<0.
(3)当a>0时,二次函数g(x)的图象开口向上,
且g(0)=-2,g(1)=-2.
所以?x0∈(1,+∞),当x∈(1,x0)时,g(x)<0. 当x∈(x0,+∞)时,g(x)>0;
所以f(x)在区间(1,+∞)内先递减再递增.
故f(x)在区间[2,e+1]上的最大值只能是f(2)或f(e+1).
∴
,即:
,
∴0<a<
.
综上:a<
.
∴f(x)=2x-
| 4 |
| x-1 |
| 2x2-2x-4 |
| x-1 |
| 2(x+1)(x-2) |
| x-1 |
令f′(x)=0,解得:x=2,
∴a=1时,f(x)的单调递增区间为(2,+∞),单调递减区间为(1,2).
(2)∵对任意m∈[2,e+1],直线PM的倾斜角都是钝角,
∴对任意m∈[2,e+1],直线PM的斜率小于0,
即
| f(m)-1 |
| m-1 |
即f(x)在区间[2,e+1]上的最大值小于1,
f(x)=
| 2(ax2-ax-2) |
| x-1 |
令g(x)=aa2-ax-2
①当a=0时,f(x)=-4ln(x-1)在[2,e+1]上单调递减,
f(x)max=f(2)=0<1,显然成立,
∴a=0.
②当a<0时,二次函数g(x)的图象开口向下,
且g(0)=-2,g(1)=-2,
?x∈(1,+∞),g(x)<0,
故f′(x)<0,f(x)在(1,+∞)上单调递减,
故f(x)在[2,e+1]上单调递减,f(x)max=f(2)=4a<0,显然成立,
∴a<0.
(3)当a>0时,二次函数g(x)的图象开口向上,
且g(0)=-2,g(1)=-2.
所以?x0∈(1,+∞),当x∈(1,x0)时,g(x)<0. 当x∈(x0,+∞)时,g(x)>0;
所以f(x)在区间(1,+∞)内先递减再递增.
故f(x)在区间[2,e+1]上的最大值只能是f(2)或f(e+1).
∴
|
|
∴0<a<
| 1 |
| 4 |
综上:a<
| 1 |
| 4 |
点评:本题考察了用导数研究函数的性质;渗透了分类讨论思想,本题是一道综合题.

练习册系列答案
相关题目
下列语句能使变量a的值为4的是( )
| A、INPUT a=4 |
| B、b=4,b=a |
| C、a=3,a=a+1 |
| D、2a=a+4 |
 在平面直角坐标系xOy中,过点P(-4,0)作直线交椭圆C:
在平面直角坐标系xOy中,过点P(-4,0)作直线交椭圆C: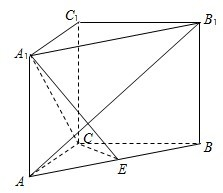 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=CB=CC1=2,E是AB中点.
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=CB=CC1=2,E是AB中点.