Question

设a∈R，函数f（x）=x|x-a|+2x．
（1）若a=2，求函数f（x）在区间[0，3]上的最大值；
（2）若a＞2，写出函数f（x）的单调区间（不必证明）；
（3）若存在a∈[3，6]，使得关于x的方程f（x）=t+2a有三个不相等的实数解，求实数t的取值范围．

Answer 1

考点：根的存在性及根的个数判断

专题：综合题,函数的性质及应用

分析：（1）通过图象直接得出；
（2）将x分区间进行讨论，去绝对值写出解析式，求出单调区间；
（3）当3≤a≤6时，由（1）知f（x）在（-∞，

a+2

2

]和[a，+∞）上分别是增函数，在[

a+2

2

，a]上是减函数，当且仅当2a＜t+2a＜

(a+2)2

4

时，方程f（x）=t+2a有三个不相等的实数解

解答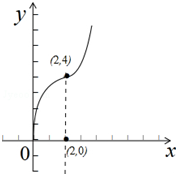： 解：（1）当a=2，x∈[0，3]时，f（x）=x|x-2|+2x=

x2，x≥2 -x2+4x，0≤x＜2

作函数图象，
可知函数f（x）在区间[0，3]上是增函数．
所以f（x）在区间[0，3]上的最大值为f（3）=9．
（2）f（x）=

x2+(2-a)x，x≥a -x2+(2+a)x，x＜a

①当x≥a时，f（x）=(x-

a-2

2

)2-

(a-2)2

4

．
因为a＞2，所以

a-2

2

＜a．
所以f（x）在[a，+∞）上单调递增．
②当x＜a时，f（x）=-(x-

a+2

2

)2+

(a+2)2

4

．
因为a＞2，所以

a+2

2

＜a．
所以f（x）在（-∞，

a+2

2

]上单调递增，在[

a+2

2

，a]上单调递减．
综上所述，函数f（x）的递增区间是（-∞，

a+2

2

]和[a，+∞），递减区间是[

a+2

2

，a]．
（3）当3≤a≤6时，由（1）知f（x）在（-∞，

a+2

2

]和[a，+∞）上分别是增函数，在[

a+2

2

，a]上是减函数，
当且仅当2a＜t+2a＜

(a+2)2

4

时，方程f（x）=t+2a有三个不相等的实数解．
即0＜t＜

(a-2)2

4

令g(a)=

(a-2)2

4

，g（a）在a∈[3，6]时是增函数，
故g（a）_max=4．
∴实数t的取值范围是（0，4）．

点评：本题考查了函数的最值，函数单调性的证明，渗透了分类讨论思想，综合性较强，是较难的一道题．