题目内容
14.(1)计算:${[{{{({3\frac{13}{81}})}^{-3}}}]^{\frac{1}{6}}}$-lg$\frac{1}{100}-{(ln\sqrt{e})^{-1}}$$+{0.1^{-2}}-{(2+\frac{10}{27})^{-\frac{2}{3}}}$$-{(\frac{1}{{2+\sqrt{3}}})^0}$$+{2^{-1-{{log}_2}\frac{1}{6}}}$(2)已知tan(π-α)=-2; 求sin2(π+α)+sin($\frac{π}{2}$+α)cos($\frac{3π}{2}$-α)的值.
分析 (1)利用对数的运算法则、分数指数幂计算法则直接计算.
(2)利用诱导公式和同角三角函数关系进行解答即可.
解答 解:(1)原式=$\sqrt{\frac{81}{256}}$+2+$\frac{1}{2}$+100-$\frac{9}{16}$-1+3
=$\frac{9}{16}$+2+$\frac{1}{2}$+100-$\frac{9}{16}$-1+3
=$\frac{209}{2}$;
(2)∵tan(π-α)=-2,
∴tanα=2.
∴sin2(π+α)+sin($\frac{π}{2}$+α)cos($\frac{3π}{2}$-α)
=sin2α+cosα•(-sinα)
=$\frac{si{n}^{2}α-cosαsinα}{si{n}^{2}α+co{s}^{2}α}$
=$\frac{ta{n}^{2}α-tanα}{ta{n}^{2}α+1}$
=$\frac{{2}^{2}-2}{{2}^{2}+1}$
=$\frac{2}{5}$.
点评 本题主要考查了根式与分数指数幂的互化及其化简运算,同角三角函数关系式和诱导公式的应用,属于基本知识的考查.

练习册系列答案
相关题目
4.下列各命题是真命题的是( )
| A. | 如果a>b,那么$\frac{a}{c}$>$\frac{b}{c}$ | B. | 如果ac<bc,那么a<b | ||
| C. | 如果a>b,c>d,那么a-c>b-d | D. | 如果a>b,那么a-c>b-c |
5.已知数列{an}的通项公式an=n2-2n-8(n∈N*),则a4等于( )
| A. | 1 | B. | 2 | C. | 0 | D. | 3 |
3.已知实数x,y满足$\left\{\begin{array}{l}x-2y-2≥0\\ 2x+y-4≥0\\ x-y-3≤0\end{array}\right.$则x2+(y+2)2的取值范围是( )
| A. | [$\frac{65}{9}$,25] | B. | [$\frac{36}{5}$,25] | C. | [16,25] | D. | [9,25] |
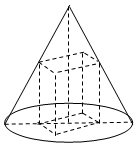 底面半径为4,高为$8\sqrt{2}$的圆锥有一个内接的正四棱柱(底面是正方形,侧棱与底面垂直的四棱柱).
底面半径为4,高为$8\sqrt{2}$的圆锥有一个内接的正四棱柱(底面是正方形,侧棱与底面垂直的四棱柱).