题目内容
10．已知等比数列{an}中，S3=20，S6=60，则S9=140．分析 由等比数列{an}的性质可得：S3，S6-S3，S9-S6，成等比数列．即可得出．
解答 解：由等比数列{an}的性质可得：S3，S6-S3，S9-S6，成等比数列．
∴（60-20）2=20×（S9-60），解得S9=140．
故答案为：140．
点评 本题考查了等比数列的通项公式与性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
20．已知集合P={1，3，5，7}，Q={x|2x-1＞11}，则P∩Q等于（ ）
| A． | {7} | B． | {5，7} | C． | {3，5，7} | D． | {x|6＜x≤7} |
18．已知正实数a，b满足a+b=3，则$\frac{1}{1+a}+\frac{4}{4+b}$的最小值为（ ）
| A． | 1 | B． | $\frac{7}{8}$ | C． | $\frac{9}{8}$ | D． | 2 |
5．已知数列{an}的通项公式an=n2-2n-8（n∈N*），则a4等于（ ）
| A． | 1 | B． | 2 | C． | 0 | D． | 3 |
15．已知角$α∈（\frac{π}{2}，π）$，且tanα=-$\frac{{\sqrt{3}}}{3}$，则cosα的值为（ ）
| A． | $-\frac{{\sqrt{3}}}{3}$ | B． | $\frac{{\sqrt{3}}}{3}$ | C． | $-\frac{{\sqrt{3}}}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
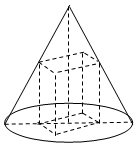底面半径为4，高为$8\sqrt{2}$的圆锥有一个内接的正四棱柱（底面是正方形，侧棱与底面垂直的四棱柱）．