题目内容
过点(-1,3)作圆(x-2)2+(y+1)2=9的切线,求切线方程.
考点:圆的切线方程
专题:应用题,直线与圆
分析:分类讨论,结合题意设直线为:kx-y+k+4=0,由点到直线的距离等于半径即可得到k,求出切线方程.
解答:
解:圆(x-2)2+(y+1)2=9的圆心与半径分别为:(2,-1);3.
当切线的斜率存在,设切线的斜率为k,则切线方程为:kx-y+k+4=0,
由点到直线的距离公式可得:
=3,
解得:k=-
,
所以切线方程为:8x+15y-37=0;
当切线的斜率不存在时,直线为:x=-1,满足圆心(2,-1)到直线x=-1的距离为圆的半径3,
所以x=-1也是切线方程;
综上,切线方程为:8x+15y-37=0或x=-1.
当切线的斜率存在,设切线的斜率为k,则切线方程为:kx-y+k+4=0,
由点到直线的距离公式可得:
| |3k+5| | ||
|
解得:k=-
| 8 |
| 15 |
所以切线方程为:8x+15y-37=0;
当切线的斜率不存在时,直线为:x=-1,满足圆心(2,-1)到直线x=-1的距离为圆的半径3,
所以x=-1也是切线方程;
综上,切线方程为:8x+15y-37=0或x=-1.
点评:本题主要考查圆的切线方程,以及点到直线的距离公式,容易疏忽斜率不存在的情况.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
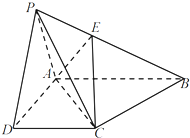 如图,四棱锥P-ABCD的底面是直角梯形,其中AB⊥AD,DC⊥AD,AB=AD=2,DC=1.侧面正△PAD所在平面与底面垂直.
如图,四棱锥P-ABCD的底面是直角梯形,其中AB⊥AD,DC⊥AD,AB=AD=2,DC=1.侧面正△PAD所在平面与底面垂直.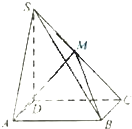 如图,四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=
如图,四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=