题目内容
 已知椭圆C:
已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)设P是l1上(除A1外)的动点,连结A2P交椭圆于另外一点B,连结OP交椭圆于C,D两点(C在D的下方),直线A1B,A1C,A1D分别交直线l2于点E,F,G,若|EF|,|A2F|,|GF|成等差数列,求点P的坐标.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)根据长轴长为2
,直线l1:y=-1与C只有一个公共点A1,直线l2:y=1与C只有一个公共点A2,求出a,b,即可求椭圆C的方程;
(Ⅱ)设P(t,-1),则直线A2P的方程,求出B的坐标,再求出E的坐标,确定直线A1C、A2D的方程,令y=1,确定F,G的坐标,利用|EF|,|A2F|,|GF|成等差数列,结合C在直线OP上,即可求出点P的坐标.
| 2 |
(Ⅱ)设P(t,-1),则直线A2P的方程,求出B的坐标,再求出E的坐标,确定直线A1C、A2D的方程,令y=1,确定F,G的坐标,利用|EF|,|A2F|,|GF|成等差数列,结合C在直线OP上,即可求出点P的坐标.
解答:
解:(I)由题意得:a=
,b=1,
∴椭圆方程为:
+y2=1…(4分)
(II)设P(t,-1),则直线A2P的方程为:y=-
x+1…(5分)
联立
消去y,得(
+
)x2-
x=0…(7分)
解得B(
,
)…(8分)
直线A1B方程为y=
x-1,令y=1,得x=
,得E(
,1)…(9分)
又直线OP的方程为y=-
x
C,D关于O(0,0)中心对称,可设C(x1,y1),D(-x1,-y1),
直线A1C、A2D的方程分别为y=
x-1,y=
x-1,
令y=1,得F(
,1),G(
,1)…11分
∴|EF|=
-
,|A2F|=-
,|GF|=
-
,…(12分)
∵|EF|,|A2F|,|GF|成等差数列,
∴
-
+
-
=-
,
化简得:
=
…..①…(13分)
又C在直线OP上,所以y1=-
x1…..②
联立①、②解得x1=
,y1=
…(14分)
又C(x1,y1)在椭圆上,代入椭圆方程得
+
=1,解得:t=±4(15分)
| 2 |
∴椭圆方程为:
| x2 |
| 2 |
(II)设P(t,-1),则直线A2P的方程为:y=-
| 2 |
| t |
联立
|
| 4 |
| t2 |
| 1 |
| 2 |
| 4 |
| t |
解得B(
| 8t |
| 8+t2 |
| -8+t2 |
| 8+t2 |
直线A1B方程为y=
| t |
| 4 |
| 8 |
| t |
| 8 |
| t |
又直线OP的方程为y=-
| 1 |
| t |
C,D关于O(0,0)中心对称,可设C(x1,y1),D(-x1,-y1),
直线A1C、A2D的方程分别为y=
| y1+1 |
| x1 |
| 1-y1 |
| -x1 |
令y=1,得F(
| 2x1 |
| y1+1 |
| -2x1 |
| 1-y1 |
∴|EF|=
| 8 |
| t |
| 2x1 |
| y1+1 |
| 2x1 |
| y1+1 |
| -2x1 |
| 1-y1 |
| 2x1 |
| y1+1 |
∵|EF|,|A2F|,|GF|成等差数列,
∴
| 8 |
| t |
| 2x1 |
| y1+1 |
| -2x1 |
| 1-y1 |
| 2x1 |
| y1+1 |
| 4x1 |
| y1+1 |
化简得:
| 8 |
| t |
| 2x1 |
| 1-y1 |
又C在直线OP上,所以y1=-
| 1 |
| t |
联立①、②解得x1=
| 4t |
| t2-4 |
| -4 |
| t2-4 |
又C(x1,y1)在椭圆上,代入椭圆方程得
| 8t2 |
| (t2-4)2 |
| 16 |
| (t2-4)2 |
点评:本题考查直线与圆锥曲线的综合问题,考查椭圆的方程,考查等差数列的性质,考查学生的计算能力,有难度.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
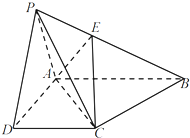 如图,四棱锥P-ABCD的底面是直角梯形,其中AB⊥AD,DC⊥AD,AB=AD=2,DC=1.侧面正△PAD所在平面与底面垂直.
如图,四棱锥P-ABCD的底面是直角梯形,其中AB⊥AD,DC⊥AD,AB=AD=2,DC=1.侧面正△PAD所在平面与底面垂直.