题目内容
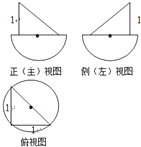 有100件规格相同的铁件(铁的密度是7.8g/cm3),该铁件的三视图如图所示,其中正视图,侧视图均是由三角形与半圆构成,俯视图由圆与内接三角形构成(图中单位cm).
有100件规格相同的铁件(铁的密度是7.8g/cm3),该铁件的三视图如图所示,其中正视图,侧视图均是由三角形与半圆构成,俯视图由圆与内接三角形构成(图中单位cm).(1)指出该几何体的形状特征;
(2)根据图中的数据,求出此几何体的体积;
(3)问这100件铁件的质量大约有多重(π取3.1,
| 2 |
考点:由三视图求面积、体积,简单空间图形的三视图
专题:空间位置关系与距离
分析:(1)由三视图可知,该几何体是个组合体;上部分是个正三棱锥,其三条侧棱两两垂直;下部分为一个半球;
(2)分别求出棱锥的体积和半球的体积,相加可得答案;
(3)计算出这100件铁件的体积和,乘以密度后可得质量.
(2)分别求出棱锥的体积和半球的体积,相加可得答案;
(3)计算出这100件铁件的体积和,乘以密度后可得质量.
解答:
解:(1)由三视图可知,该几何体是个组合体;
上部分是个正三棱锥,其三条侧棱两两垂直;
下部分为一个半球,并且正三棱锥的一个侧面与半球的底面相切.…(3分)

(2)由图可知:V三棱锥=
(
×1×1)×1=
…(5分)
球半径r=
…(6分)
V半球=
π×(
)3=
…(8分)
所以该几何体体积V=
…(9分)
(3)这100件铁件的质量m:
…(11分)
答:这批铁件的质量超过694g.…(12分)
上部分是个正三棱锥,其三条侧棱两两垂直;
下部分为一个半球,并且正三棱锥的一个侧面与半球的底面相切.…(3分)

(2)由图可知:V三棱锥=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
球半径r=
| ||
| 2 |
V半球=
| 2 |
| 3 |
| ||
| 2 |
| ||
| 6 |
所以该几何体体积V=
1+
| ||
| 6 |
(3)这100件铁件的质量m:
|
答:这批铁件的质量超过694g.…(12分)
点评:本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
相关题目
平面向量
,
满足|
|=2,|
+
|=4,且向量
与向量
+
的夹角为
,则|
|为( )
| a |
| b |
| a |
| a |
| b |
| a |
| a |
| b |
| π |
| 3 |
| b |
| A、2 | ||||
B、2
| ||||
C、2
| ||||
D、2
|
已知数列|an|满足a1+a2+a3+…+an=2n2-3n,则a5=( )
| A、9 | B、12 | C、15 | D、18 |
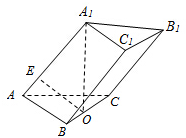 在三棱柱ABC-A1B1C1中,已知AA1=8,AC=AB=5,BC=6,点A1在底面ABC的射影是线段BC的中点O,在侧棱AA1上存在一点E,且OE⊥B1C.
在三棱柱ABC-A1B1C1中,已知AA1=8,AC=AB=5,BC=6,点A1在底面ABC的射影是线段BC的中点O,在侧棱AA1上存在一点E,且OE⊥B1C.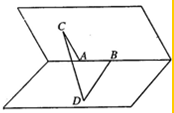 如图,60°的二面角的棱上有A,B两点,线段AC,BD分别在这个二面角的两个半平面内,且AC⊥AB,BD⊥AB,已知AB=4,AC=6,BD=8.
如图,60°的二面角的棱上有A,B两点,线段AC,BD分别在这个二面角的两个半平面内,且AC⊥AB,BD⊥AB,已知AB=4,AC=6,BD=8.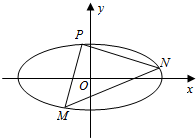 如图,椭圆C:
如图,椭圆C: