题目内容
为迎接2015年在兰州举行的“中国兰州国际马拉松比赛”,某单位在推介晚会中进行嘉宾现在抽奖活动,抽奖盒中装有大小相同的6个小球,分别印有“兰州马拉松”和“绿色金城行”两种标志,摇匀后,规定参加者每次从盒中同时抽取两个小球(登记后放回并摇匀),若抽到的两个球都印有“兰州马拉松”标志即可获奖.并停止取球;否则继续,但每位嘉宾最多抽取3次,已知从盒中抽取两个小球不都是“绿色金城行”标志的概率为
.
(Ⅰ)求盒中印有“兰州马拉松”标志的小球的个数;
(Ⅱ)若用η表示这位嘉宾抽取的次数,求η的分布列和期望.
| 4 |
| 5 |
(Ⅰ)求盒中印有“兰州马拉松”标志的小球的个数;
(Ⅱ)若用η表示这位嘉宾抽取的次数,求η的分布列和期望.
考点:离散型随机变量的期望与方差,离散型随机变量及其分布列
专题:概率与统计
分析:(Ⅰ)设印有“绿色金城行”的球有n个,同时抽两球不都是“绿色金城行”标志为事件A,由对立事件的概率:P(A)=1-P(
)=
,即P(
)=
=
,由此能求出n.
(Ⅱ)由已知,两种球各三个,η可能取值分别为1,2,3,分别求出相应的概率,由此能求出η的分布列和期望.
. |
| A |
| 4 |
| 5 |
. |
| A |
| ||
|
| 1 |
| 5 |
(Ⅱ)由已知,两种球各三个,η可能取值分别为1,2,3,分别求出相应的概率,由此能求出η的分布列和期望.
解答:
解:(Ⅰ)设印有“绿色金城行”的球有n个,
同时抽两球不都是“绿色金城行”标志为事件A,
则同时抽取两球都是“绿色金城行”标志的概率是P(
)=
,
由对立事件的概率:P(A)=1-P(
)=
,
即P(
)=
=
,解得n=3.…(6分)
(Ⅱ)由已知,两种球各三个,η可能取值分别为1,2,3,
P(η=1)=
=
,
P(η=2)=
•
+
•
=
,
P(η=3)=1-P(η=1)-P(η=2)=
,
则η 的分布列为:
所以Eη=1×
+2×
+3×
=
.…(12分)
同时抽两球不都是“绿色金城行”标志为事件A,
则同时抽取两球都是“绿色金城行”标志的概率是P(
. |
| A |
| ||
|
由对立事件的概率:P(A)=1-P(
. |
| A |
| 4 |
| 5 |
即P(
. |
| A |
| ||
|
| 1 |
| 5 |
(Ⅱ)由已知,两种球各三个,η可能取值分别为1,2,3,
P(η=1)=
| ||
|
| 1 |
| 5 |
P(η=2)=
| ||
|
| ||
|
| ||||
|
| ||
|
| 4 |
| 25 |
P(η=3)=1-P(η=1)-P(η=2)=
| 16 |
| 25 |
则η 的分布列为:
| η | 1 | 2 | 3 | ||||||
| P |
|
|
|
| 1 |
| 5 |
| 4 |
| 25 |
| 16 |
| 25 |
| 61 |
| 25 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要注意排列组合知识的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
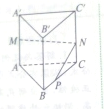 如图,在直棱柱ABC-A′B′C′中,底面是边长为3的等边三角形,AA′=4,M为AA′的中点,P是BC上一点,且由P沿棱柱侧面经过棱CC′到M的最短路线长为
如图,在直棱柱ABC-A′B′C′中,底面是边长为3的等边三角形,AA′=4,M为AA′的中点,P是BC上一点,且由P沿棱柱侧面经过棱CC′到M的最短路线长为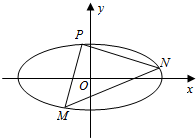 如图,椭圆C:
如图,椭圆C: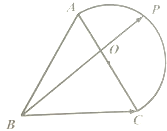 已知△ABC是边长为2的正三角形,以AC为直径作半圆O(如图),P为半圆上任一点,则
已知△ABC是边长为2的正三角形,以AC为直径作半圆O(如图),P为半圆上任一点,则