题目内容
某高校自主招生中,体育特长生的选拔考试,篮球项目初试办法规定:每位考生定点投篮,投进2球立刻停止,但投篮的总次数不能超过5次,投篮时间不能超过半分钟.某考生参加了这项测试,他投篮的命中率为0.8,假设他各次投篮之间互不影响.若记投篮的次数为ξ,求ξ的分布列和数学期望.
考点:离散型随机变量的期望与方差
专题:应用题,概率与统计
分析:由题意ξ∈{2,3,4,5},分别算出P(ξ=2),P(ξ=3),P(ξ=4),P(ξ=5),再利用期望公式求解.
解答:
解:由题意ξ∈{2,3,4,5},则
P(ξ=2)=0.8×0.8=0.64,P(ξ=3)=
×0.8×0.2×0.8=0.256,
P(ξ=4)=
×0.8×0.22×0.8=0.0768,P(ξ=5)=1-0.64-0.256-0.0768=0.0272,
所以ξ的分布列为:
所以Eξ=2×0.64+3×0.256+4×0.0768+5×0.0272=2.4912.
P(ξ=2)=0.8×0.8=0.64,P(ξ=3)=
| C | 1 2 |
P(ξ=4)=
| C | 1 3 |
所以ξ的分布列为:
| ξ | 2 | 3 | 4 | 5 |
| P | 0.64 | 0.256 | 0.0768 | 0.0272 |
点评:本小题主要考查概率计算,考查取有限个值的离散型随机变量及其分布列和均值的概念,通过设置密切贴近现实生活的情境,考查概率思想的应用意识和创新意识.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
如果α∥β,AB与AC是夹在平面α与β之间的两条线段,AB⊥AC且AB=2,直线AB与平面α所成的角为30°,那么线段AC长的取值范围是( )
A、(
| ||||||||
| B、[1,+∞) | ||||||||
C、(1,
| ||||||||
D、[
|
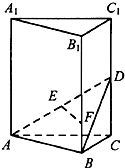 如图,在直三棱柱ABC-A1B1C1中,D、E分别为CC1、AD的中点,F为BB1上的点,且B1F=3BF
如图,在直三棱柱ABC-A1B1C1中,D、E分别为CC1、AD的中点,F为BB1上的点,且B1F=3BF
