题目内容
4.下列叙述中错误的是( )| A. | 若点P∈α,P∈β且α∩β=l,则P∈l | |
| B. | 三点A,B,C能确定一个平面 | |
| C. | 若直线a∩b=A,则直线a与b能够确定一个平面 | |
| D. | 若点A∈l,B∈l,且A∈α,B∈α,则l?α |
分析 在A中,由公理二知P∈l;在B中,三点A,B,C共线时,不能确定一个平面;在C中,由公理三知直线a与b能够确定一个平面;在D中,由公理一知l?α.
解答 解:在A中,若点P∈α,P∈β且α∩β=l,则由公理二知P∈l,故A正确;
在B中,三点A,B,C不共线时,能确定一个平面;三点A,B,C共线时,不能确定一个平面,故B错误;
在C中,若直线a∩b=A,则由公理三知直线a与b能够确定一个平面,故C正确;
在D中,若点A∈l,B∈l,且A∈α,B∈α,则由公理一知l?α,故D正确.
故选:B.
点评 本题考查命题真判断,是中档题,解题时要认真审题,注意平面的基本定理及推论的合理运用.

练习册系列答案
相关题目
14.已知向量$\overrightarrow{a}$=(cos40°,sin40°),$\overrightarrow{b}$=(sin20°,cos20°),$\overrightarrow{u}$=$\sqrt{3}$$\overrightarrow{a}$+λ$\overrightarrow{b}$(其中λ∈R),则|$\overrightarrow{u}$|的最小值为( )
| A. | $\frac{{\sqrt{6}}}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\sqrt{3}$ |
15.在正方体ABCD-A1B1C1D1中,点E,F满足$\overrightarrow{{A}_{1}E}$=3$\overrightarrow{E{B}_{1}}$,$\overrightarrow{{C}_{1}F}$=3$\overrightarrow{F{D}_{1}}$,则BE与DF所成角的正弦值为( )
| A. | $\frac{8}{17}$ | B. | $\frac{9}{17}$ | C. | $\frac{12}{17}$ | D. | $\frac{15}{17}$ |
12.长方体的一个顶点上三条棱长分别为3、4、5,且它的8个顶点都在同一球面上,则这个球的表面积是( )
| A. | 25π | B. | 50π | C. | 125π | D. | 75π |
9.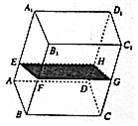 如图,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:
如图,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:
①水的部分始终呈棱柱状;
②水面四边形EFGH的面积不改变;
③棱A1D1始终与水面EFGH平行;
④当E∈AA1时,AE+BF是定值.其中正确说法的是( )
 如图,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:
如图,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:①水的部分始终呈棱柱状;
②水面四边形EFGH的面积不改变;
③棱A1D1始终与水面EFGH平行;
④当E∈AA1时,AE+BF是定值.其中正确说法的是( )
| A. | ②③④ | B. | ①②④ | C. | ①③④ | D. | ①②③ |
14.高考后,4位考生各自在甲、乙两所大学中任选一所参观,则甲、乙两所大学都有考生参观的概率为( )
| A. | $\frac{1}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{5}{8}$ | D. | $\frac{7}{8}$ |
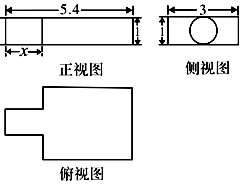 我国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器--商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其体积为12.6(立方寸),则图中的x为1.6寸.
我国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器--商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其体积为12.6(立方寸),则图中的x为1.6寸.