题目内容
对于定义域为D的函数y=f(x)和常数C,若对任意正实数ε,?x∈D,使得0<|f(x)-C|<ε恒成立,则称函数y=f(x)为“敛C函数”.现给出如下函数:
①f(x)=x(x∈Z);
②f(x)=(
)x+1(x∈Z);
③f(x)=log3x;
④f(x)=
.
其中为“敛1函数”的有( )
①f(x)=x(x∈Z);
②f(x)=(
| 1 |
| 3 |
③f(x)=log3x;
④f(x)=
| x-1 |
| x |
其中为“敛1函数”的有( )
| A、①② | B、③④ | C、②④ | D、①②③ |
考点:对数函数的单调性与特殊点,函数的值域
专题:新定义,函数的性质及应用
分析:由题意可得,“敛1函数”满足对任意正实数ε,?x∈D,使|f(x)-1|<ε恒成立,即使得|f(x)-1|∈R+,对选项进行验证即可.
解答:
解:由题意可得,“敛1函数”满足对任意正实数ε,?x∈D,使|f(x)-1|<ε恒成立,即使得|f(x)-1|∈R+,
①f(x)=x(x∈Z),则|f(x)-1|≥1,所以不满足“敛1函数”的定义;
②f(x)=(
)x+1,则|f(x)-1|=|(
)x|∈R+,满足对任意正实数ε,?x∈D,使|f(x)-1|<ε恒成立;
③f(x)=log3x,则|f(x)-1|=|log3x-1|≥0,所以不满足“敛1函数”的定义;
④f(x)=
,则|f(x)-1|=|
|∈R+,满足对任意正实数ε,?x∈D,使|f(x)-1|<ε恒成立.
故选:D.
①f(x)=x(x∈Z),则|f(x)-1|≥1,所以不满足“敛1函数”的定义;
②f(x)=(
| 1 |
| 3 |
| 1 |
| 3 |
③f(x)=log3x,则|f(x)-1|=|log3x-1|≥0,所以不满足“敛1函数”的定义;
④f(x)=
| x-1 |
| x |
| 1 |
| x |
故选:D.
点评:本题利用新定义,考查函数性质,解题的关键是正确理解“敛1函数”,利用使得|f(x)-1|∈R+进行验证.

练习册系列答案
相关题目
设x,y满足条
,若目标函数z=ax+by(a>0,b>0)的最小值为2,则ab的最大值为( )
|
| A、1 | ||
B、
| ||
C、
| ||
D、
|
如果某物体的运动方程为s=2(1-t2)(s的单位为m,t的单位为s),那么其在1.2s末的瞬时速度为( )
| A、-4.8m/s |
| B、-2.8m/s |
| C、0.88 m/s |
| D、4.8 m/s |
 某四棱锥的三视图如图所示,记A为此棱锥所有棱的长度的集合,则( )
某四棱锥的三视图如图所示,记A为此棱锥所有棱的长度的集合,则( )| A、2∈A,且4∈A | ||||
B、
| ||||
C、2∈A,且2
| ||||
D、
|
若在△ABC中,有sin
=cosA,则△ABC一定是( )
| C |
| 2 |
| A、锐角三角形 |
| B、钝角三角形 |
| C、直角三角形 |
| D、等腰三角形 |
若{an}为等差数列,Sn是其前n项和,且S13=
π,则tana7的值为( )
| 13 |
| 4 |
| A、-1 | ||||
B、-
| ||||
C、±
| ||||
| D、1 |
对于任意x∈[-1,0],恒有
x3-x2-3x-2m≤3成立,则m的取值范围为( )
| 1 |
| 3 |
A、[-
| ||
| B、[-1,+∞) | ||
C、[-
| ||
| D、[-2,+∞) |
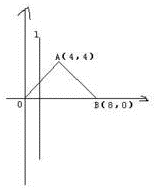 如图,直线l⊥x轴,从原点开始向右平行移动到x=8处停止,它扫过△AOB所得图形的面积为S,它与x轴的交点为(x,0).
如图,直线l⊥x轴,从原点开始向右平行移动到x=8处停止,它扫过△AOB所得图形的面积为S,它与x轴的交点为(x,0).