题目内容
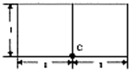若一个底面是等腰直角三角形（C为直角顶点）的三棱柱的正视图如图所示，则该三棱柱的体积等于（ ）A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：根据三棱柱的正视图判断三棱柱的高及底面等腰直角三角形的斜边长，求出直角边长，把数据代入棱柱的体积公式计算．
解答：
解：由三棱柱的正视图可得．三棱柱的高为1，
底面等腰直角三角形的斜边长为2，∴直角边长为
，
∴三棱柱的体积V=
×
×
×1=1．
故选：B．
底面等腰直角三角形的斜边长为2，∴直角边长为
| 2 |
∴三棱柱的体积V=
| 1 |
| 2 |
| 2 |
| 2 |
故选：B．
点评：本题考查了由正视图求几何体的体积，解题的关键是判断正视图的数据所对应的几何量．
练习册系列答案
一本好题口算题卡系列答案
相关题目
已知集合M={y|y=2x，x＞0}，N={y|y=
}，则M∩N等于（ ）
| 2x-x2 |
| A、∅ | B、{1} |
| C、{y|y＞1} | D、{y|y≥1} |
函数f（x）=（
）x-2-x3的零点所在的区间为（ ）
| 1 |
| 2 |
| A、（0，1） |
| B、（1，2） |
| C、（2，3） |
| D、（3，4） |
圆x2+y2+2x-4y=0的圆心坐标为（ ）
| A、（-1，2） |
| B、（-1，-2） |
| C、（1，-2） |
| D、（1，2） |
在区间[-4，2]上随机取一个数，则该数是正数的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
函数y=sinx+
cosx的最大值是（ ）
| 3 |
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
函数y=x•2x的部分图象如下，其中正确的是（ ）
A、 |
B、 |
C、 |
D、 |
若a是复数z1=
的实部，b是复数z2=（1-i）3的虚部，则ab等于（ ）
| 1+i |
| 2-i |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
如图，某园林公司计划在一块半径为定值R（单位：优）的半圆形土地上种植花木、草皮，其中弓形CMD区域用于种植花草样品供人观赏，△OCD（O为圆心）区域用于种植花木出售，扇形O