题目内容
在区间[-4,2]上随机取一个数,则该数是正数的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:计算题,概率与统计
分析:根据几何概型公式,将符合题意的区间长度除以总的区间长度,即得本题的概率.
解答:
解:记事件A=“该数为正数”,
∵区间[-4,2]长度是6,该数为正数的取值区间长度是2,
∴由几何概型公式,得P(A)=
=
故选:C.
∵区间[-4,2]长度是6,该数为正数的取值区间长度是2,
∴由几何概型公式,得P(A)=
| 2 |
| 6 |
| 1 |
| 3 |
故选:C.
点评:本题主要考查了几何概型和概率的意义等知识,解题的关键是利用几何概型公式,属于基础题.

练习册系列答案
相关题目
i5(1-i)=( )
| A、1+i | B、i-1 |
| C、2i | D、-2 |
“m=
”是“直线(m+2)x+3my+1=0与直线(m+2)x+(m-2)y-3=0相互垂直”的( )
| 1 |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要 |
清华大学给安阳市某三所重点中学6个自主招生的推荐名额,则每所中学至少分到一个名额的不同方法数为( )
| A、10 | B、18 |
| C、20 | D、64 |
在等差数列{an}中,a6=10,S5=5,则a8=( )
| A、18 | B、15 | C、16 | D、17 |
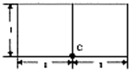 若一个底面是等腰直角三角形(C为直角顶点)的三棱柱的正视图如图所示,则该三棱柱的体积等于( )
若一个底面是等腰直角三角形(C为直角顶点)的三棱柱的正视图如图所示,则该三棱柱的体积等于( )A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|
复数
在复平面内对应的点与原点的距离为( )
| i2+i3+i4 |
| 1-i |
| A、1 | ||||
B、
| ||||
C、
| ||||
| D、2 |
设U=R,M={x|x2-x≤0},函数f(x)=
的定义域为D,则M∩(∁UD)=( )
| 1 | ||
|
| A、[0,1) | B、(0,1) |
| C、[0,1] | D、{1} |