题目内容
函数y=sinx+
cosx的最大值是（ ）
| 3 |
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
考点：两角和与差的正弦函数
专题：三角函数的求值,三角函数的图像与性质
分析：利用两角和公式对函数解析式化简，利用三角函数的性质求得其最大值．
解答：
解：y=sinx+
cosx=2（
sinx+
cosx）=2sin（x+
）≤2，
∴函数y=sinx+
cosx的最大值是2，
故选D．
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
∴函数y=sinx+
| 3 |
故选D．
点评：本题主要考查了两角和公式的运用，三角函数的图象与性质．解题的过程注意利用拼凑法，凑出两角和公式的形式来．
练习册系列答案
相关题目
执行如图程序框图，如果输入的依次为3，5，3，5，5，4，4，3，4，4，则输出的s为（ ）
A、
| ||||
| B、4 | ||||
C、
| ||||
D、
|
已知sinα＜0，cosα＜0，则角α是（ ）
| A、第一象限的角 |
| B、第二象限的角 |
| C、第三象限的角 |
| D、第四象限的角 |
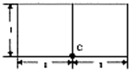若一个底面是等腰直角三角形（C为直角顶点）的三棱柱的正视图如图所示，则该三棱柱的体积等于（ ）A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|
已知2log6x=1-log63，则x的值是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知P、Q是椭圆3x2+5y2=1满足∠POQ=90°的两个动点，则
+
等于（ ）
| 1 |
| OP2 |
| 1 |
| OQ2 |
| A、34 | ||
| B、8 | ||
C、
| ||
D、
|
已知α，β表示两个相交的平面，直线l在平面α内且不是平面α，β的交线，则“l⊥β”是“α⊥β”的（ ）
| A、充分条件 |
| B、必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |