题目内容
在平面直角坐标系xOy中,已知动点P(x,y)(y≤0)到点F(0,-2)的距离为d1,到x轴的距离为d2,且d1-d2=2.
(Ⅰ)求点P的轨迹E的方程;
(Ⅱ)若直线l斜率为1且过点(1,0),其与轨迹E交于点M、N,求|MN|的值.
(Ⅰ)求点P的轨迹E的方程;
(Ⅱ)若直线l斜率为1且过点(1,0),其与轨迹E交于点M、N,求|MN|的值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由题意可得:
=(x,y+2),根据|PF|-|y|=2 及 y≤0,得
-|y|=2,化简可得动点P的轨迹E的方程.
(Ⅱ)直线l的方程为:y=x-1,联立
,得x2+8x-8=0,由此利用椭圆弦长公式能求出|MN|的值.
| PF |
| x2+(y+2)2 |
(Ⅱ)直线l的方程为:y=x-1,联立
|
解答:
解:(Ⅰ):(Ⅰ)由题意得:
=(x,y+2),
根据|PF|-|y|=2 及 y≤0,得
-|y|=2,
化简,整理得x2=-8y(y≤0).
所求动点P的轨迹E的方程x2=-8y(y≤0).
(Ⅱ)∵直线l斜率为1且过点(1,0),
∴直线l的方程为:y=x-1,
联立
,得x2+8x-8=0,
设M(x1,y1),N(x2,y2),则x1+x2=-8,x1x2=-8,
∴|MN|=
•
=
•
=8
.
| PF |
根据|PF|-|y|=2 及 y≤0,得
| x2+(y+2)2 |
化简,整理得x2=-8y(y≤0).
所求动点P的轨迹E的方程x2=-8y(y≤0).
(Ⅱ)∵直线l斜率为1且过点(1,0),
∴直线l的方程为:y=x-1,
联立
|
设M(x1,y1),N(x2,y2),则x1+x2=-8,x1x2=-8,
∴|MN|=
| 1+k2 |
| (x1+x2)2-4x1•x2 |
| 2 |
| (-8)2-4(-8) |
| 3 |
点评:本题考查点的轨迹方程的求法,考查弦长的求法,解题时要认真审题,注意椭圆弦长公式的合理运用.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
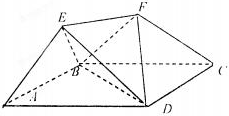 如图,底面ABCD是边长为2的菱形,且∠BAD=
如图,底面ABCD是边长为2的菱形,且∠BAD=
