题目内容
现在有6个节目准备参加比赛,其中4个舞蹈节目,2个语言类节目,如果不放回地依次抽取2个节目,求:
(1)第1次抽到舞蹈节目的概率;
(2)第1次和第2次都抽到舞蹈节目的概率;
(3)在第1次抽到舞蹈节目的条件下,第二次抽到舞蹈节目的概率.
(1)第1次抽到舞蹈节目的概率;
(2)第1次和第2次都抽到舞蹈节目的概率;
(3)在第1次抽到舞蹈节目的条件下,第二次抽到舞蹈节目的概率.
考点:相互独立事件的概率乘法公式,互斥事件的概率加法公式,条件概率与独立事件
专题:概率与统计
分析:(1)节目总数6个,其中4个舞蹈节目,2个语言类节目,由此求得第1次抽到舞蹈节目的概率.
(2)根据节目总数6个,其中4个舞蹈节目,2个语言类节目,求得第1次和第2次都抽到舞蹈节目的概率
×
.
(3)在第1次抽到舞蹈节目的条件下,这是还有5个节目,其中3个为舞蹈节目,2个为语言类节目,
由此求得第二次抽到舞蹈节目的概率.
(2)根据节目总数6个,其中4个舞蹈节目,2个语言类节目,求得第1次和第2次都抽到舞蹈节目的概率
| 4 |
| 6 |
| 3 |
| 5 |
(3)在第1次抽到舞蹈节目的条件下,这是还有5个节目,其中3个为舞蹈节目,2个为语言类节目,
由此求得第二次抽到舞蹈节目的概率.
解答:
解:(1)由题意可得,节目总数6个,其中4个舞蹈节目,2个语言类节目,
第1次抽到舞蹈节目的概率为
=
.
(2)由于节目总数6个,其中4个舞蹈节目,2个语言类节目,
故第1次和第2次都抽到舞蹈节目的概率
×
=
.
(3)在第1次抽到舞蹈节目的条件下,这是还有5个节目,其中3个为舞蹈节目,2个为语言类节目,
故第二次抽到舞蹈节目的概率为
.
第1次抽到舞蹈节目的概率为
| 4 |
| 6 |
| 2 |
| 3 |
(2)由于节目总数6个,其中4个舞蹈节目,2个语言类节目,
故第1次和第2次都抽到舞蹈节目的概率
| 4 |
| 6 |
| 3 |
| 5 |
| 2 |
| 5 |
(3)在第1次抽到舞蹈节目的条件下,这是还有5个节目,其中3个为舞蹈节目,2个为语言类节目,
故第二次抽到舞蹈节目的概率为
| 3 |
| 5 |
点评:本题主要考查古典概率、相互独立事件的概率乘法公式、条件概率的求法,属于中档题.

练习册系列答案
相关题目
复数z=
,则
=( )
| 2 |
| 1-i |
. |
| z |
| A、1+i | B、1-i |
| C、-1+i | D、-1-i |
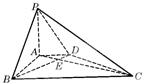 如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°PA⊥平面,PA=4,AD=2,AB=2
如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°PA⊥平面,PA=4,AD=2,AB=2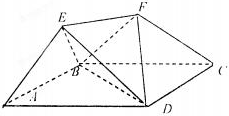 如图,底面ABCD是边长为2的菱形,且∠BAD=
如图,底面ABCD是边长为2的菱形,且∠BAD=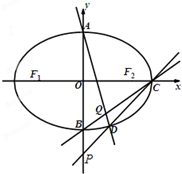 已知F1,F2分别是椭圆E:
已知F1,F2分别是椭圆E: