题目内容
已知直线2x+y-2=0和mx-y+1=0的夹角为
，则m的值为 ．
| π |
| 4 |
考点：两直线的夹角与到角问题
专题：直线与圆
分析：由条件利用两条直线的夹角公式，求得m的值．
解答：
解：由直线2x+y-2=0和mx-y+1=0的夹角为
，它们的斜率分别为-2、m，可得tan
=1=|
|，
求得m=-
或3，
故答案为：-
或3．
| π |
| 4 |
| π |
| 4 |
| m-(-2) |
| 1+m•(-2) |
求得m=-
| 1 |
| 3 |
故答案为：-
| 1 |
| 3 |
点评：本题主要考查两条直线的夹角公式的应用，属于基础题．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
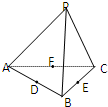空间四边形PABC的各边及对角线长度都相等，D、E、F分别是AB、BC、CA的中点，下列四个结论中不成立的是（ ）| A、DF∥平面PBC |
| B、AB⊥平面PDC |
| C、平面PEF⊥平面ABC |
| D、平面PAE平面PBC |
过曲线y=x3+1上一点（1，0）且与该点处的切线垂直的直线方程是（ ）
| A、y=3x-3 | ||||
B、y=
| ||||
C、y=-
| ||||
| D、y=-3x+3 |
数列{an}满足an+1=
，a8=2，则a1=（ ）
| 1 |
| 1-an |
| A、0 | ||
B、
| ||
| C、2 | ||
| D、-1 |