题目内容
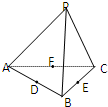空间四边形PABC的各边及对角线长度都相等，D、E、F分别是AB、BC、CA的中点，下列四个结论中不成立的是（ ）| A、DF∥平面PBC |
| B、AB⊥平面PDC |
| C、平面PEF⊥平面ABC |
| D、平面PAE平面PBC |
考点：平面与平面垂直的判定
专题：证明题,空间位置关系与距离
分析：对四个结论分别进行判断即可得出结论．
解答：
解：∵空间四边形PABC的各边及对角线长度都相等，
D、E、F、G分别是AB、BC、CA、AP的中点，
∴BC∥DF，又DF?平面PBC，BC?平面PBC，
∴BDF∥平面PBC，故A正确；
∵PD⊥AB，CD⊥AB，PD∩CD=D，
∴AB⊥平面PDC，故B正确；
∵DE⊥BC，AE⊥BC，DE∩AE=E，
∴BC⊥平面PAE，
∵BC?平面ABC，
∴平面PAE⊥平面ABC，故D正确．
故选：C．
D、E、F、G分别是AB、BC、CA、AP的中点，
∴BC∥DF，又DF?平面PBC，BC?平面PBC，
∴BDF∥平面PBC，故A正确；
∵PD⊥AB，CD⊥AB，PD∩CD=D，
∴AB⊥平面PDC，故B正确；
∵DE⊥BC，AE⊥BC，DE∩AE=E，
∴BC⊥平面PAE，
∵BC?平面ABC，
∴平面PAE⊥平面ABC，故D正确．
故选：C．
点评：本题考查命题真假的判断，是中档题，解题时要注意空间思维能力的培养．
练习册系列答案
相关题目
为使直线y=
x+b和曲线4x2-y2=36有两个交点，则b的取值范围是（ ）
| 5 |
| 2 |
A、|b|＞
| ||
B、b＜
| ||
C、b＜
| ||
D、|b|＞
|