题目内容
已知全集U=R，集合A={x|
≤2x＜2}，函数f（x）=log2（x+3）的定义域为B．求：
（Ⅰ）A∩B，A∪B；
（Ⅱ）A∩（∁UB）．
| 1 |
| 8 |
（Ⅰ）A∩B，A∪B；
（Ⅱ）A∩（∁UB）．
考点：交、并、补集的混合运算
专题：集合
分析：根据指数函数、对数函的性质分别解出集合A、B，再求解A∩B，A∪B，A∩（∁UB）．
解答：
解：由已知：A={x|-3≤x＜1}，f（x）=log2（x+3）的定义域为B={x|x＞-3}，
（Ⅰ）A∩B={x|-3＜x＜1}，A∪B={x|x≥-3}；
（Ⅱ）∁UB={x|x≤-3}，
∴A∩（∁UB）={x|x＜1}．
（Ⅰ）A∩B={x|-3＜x＜1}，A∪B={x|x≥-3}；
（Ⅱ）∁UB={x|x≤-3}，
∴A∩（∁UB）={x|x＜1}．
点评：本题主要考察集合的交、并、补集的运算，属于基础题．
练习册系列答案
相关题目
曲线y=x3-x+3在点（1，3）处的切线的斜率等于（ ）
| A、2 | B、4 | C、12 | D、6 |
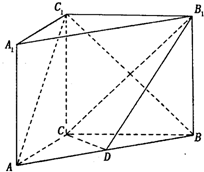如图，在直三棱柱ABC-A1B1C1中，AC=3，BC=4，AB=5，AA1=4，点D是AB的中点，
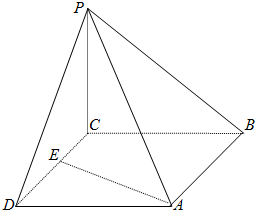如图，四棱锥P-ABCD的底面为正方形，平面PCD⊥平面ABCD，平面PBC⊥平面ABCD，E为线段CD上任意一点（不包括端点）．
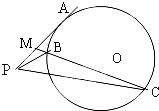如图，PA是圆O的切线，切点为A，过PA的中点M作割线交圆O于点B和C．