题目内容
已知a是实数,函数f(x)=ax2+2ax-1-a,如果函数y=f(x)的图象在区间(-2,2)上与x轴有交点,求实数a的取值范围.
考点:二次函数的性质
专题:函数的性质及应用
分析:分类讨论(1)若a=0,f(x)=-1,可得函数y=f(x)在区间(-2,2)上没有零点;
(2)当a≠0时,令f(x)=0,然后分离变量,转化为
=x2+2x-1在(-2,2)上有解.
(2)当a≠0时,令f(x)=0,然后分离变量,转化为
| 1 |
| a |
解答:
解:(1)若a=0,则f(x)=-1,∴函数y=f(x)在区间[-1,1]上没有零点,故a≠0,
(2)当a≠0时,令f(x)=0,转化为
=x2+2x-1在(-2,2)上有解,
设y=
和函数y=x2+2x-1在(-2,2)上有公共点,由x2+2x-1∈[-2,7),
要使y=
和函数y=x2+2x-1在(-2,2)上有公共点,
只要
∈[-2,7),
∴a∈(-∞,-
,]∪(
,+∞).
(2)当a≠0时,令f(x)=0,转化为
| 1 |
| a |
设y=
| 1 |
| a |
要使y=
| 1 |
| a |
只要
| 1 |
| a |
∴a∈(-∞,-
| 1 |
| 2 |
| 1 |
| 7 |
点评:本题考查函数与x轴的交点即函数的零点,涉及分类讨论的思想,主要考查函数的零点及函数的零点存在性定理,函数的零点的研究就可转化为相应方程根的问题,也可以分离变量,转化为函数图象的交点个数问题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
已知a=lgx,则a+3等于( )
| A、lg(3x) |
| B、lg(3+x) |
| C、lgx3 |
| D、lg(1000x) |
曲线y=x3-x+3在点(1,3)处的切线的斜率等于( )
| A、2 | B、4 | C、12 | D、6 |
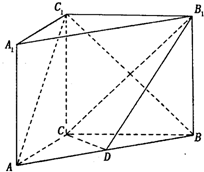 如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点,
如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点,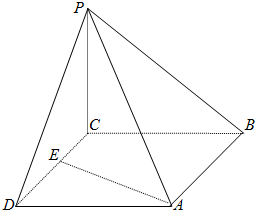 如图,四棱锥P-ABCD的底面为正方形,平面PCD⊥平面ABCD,平面PBC⊥平面ABCD,E为线段CD上任意一点(不包括端点).
如图,四棱锥P-ABCD的底面为正方形,平面PCD⊥平面ABCD,平面PBC⊥平面ABCD,E为线段CD上任意一点(不包括端点).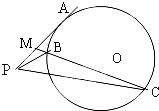 如图,PA是圆O的切线,切点为A,过PA的中点M作割线交圆O于点B和C.
如图,PA是圆O的切线,切点为A,过PA的中点M作割线交圆O于点B和C.