题目内容
已知函数f(x)=|a-
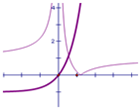
|,a>0,b>0,x≠0,且满足:函数y=f(x)的图象与直线y=1有且只有一个交点.
(1)求实数a的值;
(2)若关于x的不等式f(x)<4x-1的解集为(
,+∞),求实数b的值;
(3)在(2)成立的条件下,是否存在m,n∈R,m<n,使得f(x)的定义域和值域均为[m,n],若存在,求出m,n的值,若不存在,请说明理由.
| 1 |
| x |
(1)求实数a的值;
(2)若关于x的不等式f(x)<4x-1的解集为(
| 1 |
| 2 |
(3)在(2)成立的条件下,是否存在m,n∈R,m<n,使得f(x)的定义域和值域均为[m,n],若存在,求出m,n的值,若不存在,请说明理由.
考点:函数恒成立问题
专题:综合题,函数的性质及应用
分析:(1)依题意,a-
=-1时方程必有一根
,而a-
=1无解,从而可求得a;
(2)由f(x)=|1-
|与y=4x-1的图象知两图象的交点横坐标为
,从而可求得b;
(3)f(x)=|1-
|≥0,故必须满足n>m>0,f(1)=0,值域[m,n]中不包括0,定义域[m,n]中不包括1,只需讨论:当0<m<n<1与1<m<n时,由f(x)在[m,n]上的单调性即可求得答案.
| b |
| x |
| b |
| a+1 |
| b |
| x |
(2)由f(x)=|1-
| b |
| x |
| 1 |
| 2 |
(3)f(x)=|1-
| 1 |
| x |
解答:
 解:(1)a-
解:(1)a-
=1或a=1,因为a>0,b>0,所以a-
=-1时方程必有一根
,
因此a-
=1无解,a=1(或通过说明图象平移直接得到); …(4分)
(2)由f(x)=|1-
|与y=4x-1的图象知两图象的交点横坐标为
,
代入y=4x-1,知道交点为(
,1),
代入f(x)=|1-
|知b=1.…(9分)
(3)f(x)=|1-
|,因为f(x)≥0,所以必须满足n>m>0
又f(1)=0,值域[m,n]中不包括0,所以定义域[m,n]中不包括1,只需讨论:
当0<m<n<1时,f(x)=
-1,在[m,n]上递减,
-1=n,
-1=m,
作差得
-
=n-m,mn=1,不成立;
当1<m<n时,f(x)=1-
,在[m,n]上递增,1-
=m,1-
=n,
作差得
-
=m-n,mn=1,不成立.
综上:不存在m,n∈R,m<n满足题意. …(14分)
 解:(1)a-
解:(1)a-| b |
| x |
| b |
| x |
| b |
| a+1 |
因此a-
| b |
| x |
(2)由f(x)=|1-
| b |
| x |
| 1 |
| 2 |
代入y=4x-1,知道交点为(
| 1 |
| 2 |
代入f(x)=|1-
| b |
| x |
(3)f(x)=|1-
| 1 |
| x |
又f(1)=0,值域[m,n]中不包括0,所以定义域[m,n]中不包括1,只需讨论:
当0<m<n<1时,f(x)=
| 1 |
| x |
| 1 |
| m |
| 1 |
| n |
作差得
| 1 |
| m |
| 1 |
| n |
当1<m<n时,f(x)=1-
| 1 |
| x |
| 1 |
| m |
| 1 |
| n |
作差得
| 1 |
| n |
| 1 |
| m |
综上:不存在m,n∈R,m<n满足题意. …(14分)
点评:本题考查带绝对值的函数,着重考查数形结合思想与分类讨论思想的综合运用,考查创新能力与抽象思维能力,属于难题.

练习册系列答案
相关题目
下列图形中不一定是平面图形的是( )
| A、三角形 |
| B、梯形 |
| C、两组对边分别相等的四边形 |
| D、两组对边分别平行的四边形 |
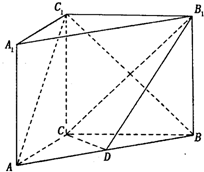 如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点,
如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点,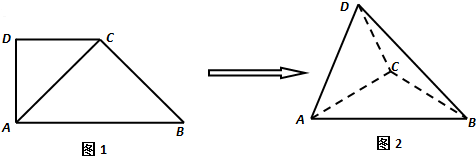
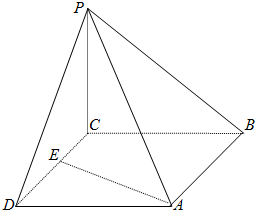 如图,四棱锥P-ABCD的底面为正方形,平面PCD⊥平面ABCD,平面PBC⊥平面ABCD,E为线段CD上任意一点(不包括端点).
如图,四棱锥P-ABCD的底面为正方形,平面PCD⊥平面ABCD,平面PBC⊥平面ABCD,E为线段CD上任意一点(不包括端点).