题目内容
6.正三棱锥P-ABC中,(△ABC是正三角形,点P在平面ABC的射影是△ABC的中心)侧棱PA与底面ABC成60°角,若AB=2$\sqrt{3}$,则P到平面ABC的距离是2$\sqrt{3}$.分析 三棱锥P-ABC的侧棱与底面ABC所成的角都是60°,利用底面正三角形的边长,转化求出棱锥的高即可.
解答  解:∵三棱锥O-ABC的侧棱与底面ABC所成的角都是60°,
解:∵三棱锥O-ABC的侧棱与底面ABC所成的角都是60°,
∴P-ABC是正三棱锥.
过P作PG⊥平面ABC交于点G,延长AG交BC于D.
∵P-ABC是正三棱锥,
∴点G是△ABC的中心,
∴AD是等边△ABC的一条高,AB=2$\sqrt{3}$,
∴AD=$\frac{\sqrt{3}}{2}×2\sqrt{3}$=3,AG=$\frac{2}{3}×3$=2,
∵PG⊥平面ABC,
侧棱PA与底面ABC成60°角,∠PAG=60°.
∴PG=AGtan60°=2$\sqrt{3}$.
则P到平面ABC的距离是:2$\sqrt{3}$.
故答案为:2$\sqrt{3}$.
点评 本题考查三棱锥的高的求法,解题时要认真审题,注意合理地化立体问题为平面问题.

练习册系列答案
相关题目
17.已知g(x)=ex(cosx+a)(a∈R)是R上的增函数,则实数a的取值范围为( )
| A. | [2,+∞) | B. | (2,+∞) | C. | [$\sqrt{2}$,+∞) | D. | ($\sqrt{2}$,+∞) |
14.已知函数f(x)=$\left\{\begin{array}{l}{3^{x+1}}(x≤0)\\{log_2}x(x>0)\end{array}$,则不等式f(x)>3的解集为( )
| A. | (8,+∞) | B. | (-∞,0)∪(8,+∞) | C. | (0,8) | D. | (-∞,0)∪(0,8) |
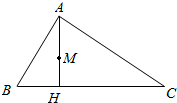 如图,在△ABC中,AB=2,BC=3,∠ABC=60°,AH⊥BC于点H,M为AH的中点,若$\overrightarrow{AM}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{BC}$,则λ+μ=$\frac{2}{3}$.
如图,在△ABC中,AB=2,BC=3,∠ABC=60°,AH⊥BC于点H,M为AH的中点,若$\overrightarrow{AM}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{BC}$,则λ+μ=$\frac{2}{3}$.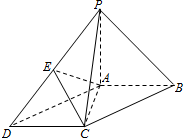 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且AB=AC=$\frac{1}{2}$PA=1,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且AB=AC=$\frac{1}{2}$PA=1,点E是PD的中点.