题目内容
15.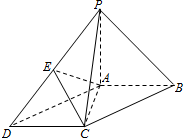 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且AB=AC=$\frac{1}{2}$PA=1,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且AB=AC=$\frac{1}{2}$PA=1,点E是PD的中点.(1)求PB与EC所成角的余弦值;
(2)求二面角E-AC-D的余弦值.
分析 (1)连BD交AC于点O,连EO,EC,说明PB与EC所成角就是∠CEO,利用余弦定理求解即可.
(2)取AD的中点F,连EF,FO,根据定义可知∠EOF是二面角E-AC-D的平面角,在△EOF中求出此角.
解答 解: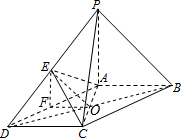 (1)连BD交AC于点O,连EO,EC,
(1)连BD交AC于点O,连EO,EC,
则EO是△PDB的中位线,PB∥EO,
PB与EC所成角就是∠CEO,
AB=AC=$\frac{1}{2}$PA=1,可得AG=FC=$\frac{\sqrt{2}}{2}$,PA=2,EF=1,EC=$\sqrt{1+\frac{1}{2}}$=$\frac{\sqrt{6}}{2}$,
OE=$\sqrt{1+({\frac{1}{2})}^{2}}$=$\frac{\sqrt{5}}{2}$,OC=1,
cos∠CEO=$\frac{\frac{5}{4}+\frac{6}{4}-1}{2×\frac{\sqrt{5}}{2}×\frac{\sqrt{6}}{2}}$=$\frac{7\sqrt{30}}{60}$.
(2)连BD交AC于点O,连EO,EC,
则EO是△PDB的中位线,
取AD的中点F,连EF,FO,
则EF是△PAD的中位线,
∴EF∥PA又PA⊥平面ABCD,
∴EF⊥平面ABCD
同理FO是△ADC的中位线,
∴FO∥AB,FO⊥AC由三垂线定理可知∠EOF是二面角E-AC-D的平面角.
又FO=$\frac{1}{2}$AB=$\frac{1}{2}$PA=EF
∴∠EOF=45°,故所求二面角E-AC-D的大小为45°.
点评 本题主要考查了直线与平面平行的判定,异面直线所成角以及二面角等有关知识,考查空间想象能力、运算能力和推理论证能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.正三棱锥P-ABC中,(△ABC是正三角形,点P在平面ABC的射影是△ABC的中心)侧棱PA与底面ABC成60°角,若AB=2$\sqrt{3}$,则P到平面ABC的距离是2$\sqrt{3}$.
3.一质点按规律S(t)=2t3+1运动,则t=1时的瞬时速度为( )
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
20.若A={2,3,4},B={x|x<4},则集合A∩B中的元素个数是( )
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
7.已知命题p:函数y=2-ax+1(a>0,a≠1)恒过定点(-1,1):命题q:若函数f(x-1)为偶函数,则f(x)的图象关于直线x=1对称.下列命题为真命题的是( )
| A. | p∧q | B. | ?p∧?q | C. | ?p∧q | D. | p∧?q |
4.正三棱柱ABC-A1B1C1各棱长均为1,M为CC1的中点,则点B1到截面A1BM的距离为( )
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
5.“抛物线y=ax2的准线方程为y=2”是“抛物线y=ax2的焦点与双曲线$\frac{y^2}{3}-{x^2}=1$的焦点重合”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
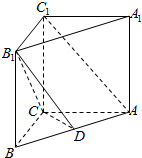 直棱柱ABC-A1B1C1中,AB=5,AC=4,BC=3,AA1=4,点D在AB上.
直棱柱ABC-A1B1C1中,AB=5,AC=4,BC=3,AA1=4,点D在AB上.