题目内容
14.设F1,F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左,右焦点,O为坐标原点,若双曲线右支上存在一点P,使$\overrightarrow{O{F}_{2}}$•$\overrightarrow{{F}_{2}P}$=0,且|$\overrightarrow{{F}_{1}{F}_{2}}$|=|$\overrightarrow{P{F}_{2}}$|,则该双曲线的离心率为$\sqrt{2}$+1.分析 由题意,P(c,2c),代入双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,可得e4-6e2+1=0,即可得出双曲线的离心率.
解答 解:由题意,P(c,2c),
代入双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,可得$\frac{{c}^{2}}{{a}^{2}}$-$\frac{4{c}^{2}}{{b}^{2}}$=1,
∴e4-6e2+1=0
∴e=$\sqrt{2}$+1.
故答案为:$\sqrt{2}$+1.
点评 本题着重考查了双曲线的定义与简单几何性质等知识,考查学生的计算能力,属于中档题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
5.函数f(x)=$\sqrt{x+1}$-ln(2-x)的定义域为( )
| A. | (2,+∞) | B. | (-1,+∞) | C. | [-1,2) | D. | (-1,2) |
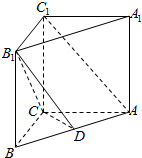 直棱柱ABC-A1B1C1中,AB=5,AC=4,BC=3,AA1=4,点D在AB上.
直棱柱ABC-A1B1C1中,AB=5,AC=4,BC=3,AA1=4,点D在AB上.