题目内容
14. 如图,圆O是一半径为10米的圆形草坪,为了满足周边市民跳广场舞的需要,现规划在草坪上建一个广场,广场形状如图中虚线部分所示的曲边四边形,其中A,B两点在⊙O上,A,B,C,D恰是一个正方形的四个顶点.根据规划要求,在A,B,C,D四点处安装四盏照明设备,从圆心O点出发,在地下铺设4条到A,B,C,D四点线路OA,OB,OC,OD.
如图,圆O是一半径为10米的圆形草坪,为了满足周边市民跳广场舞的需要,现规划在草坪上建一个广场,广场形状如图中虚线部分所示的曲边四边形,其中A,B两点在⊙O上,A,B,C,D恰是一个正方形的四个顶点.根据规划要求,在A,B,C,D四点处安装四盏照明设备,从圆心O点出发,在地下铺设4条到A,B,C,D四点线路OA,OB,OC,OD.(1)若正方形边长为10米,求广场的面积;
(2)求铺设的4条线路OA,OB,OC,OD总长度的最小值.
分析 (1)连接AB,求出正方形的面积,再求出弓形面积,作和得答案;
(2)过O作OK⊥CD,垂足为K,过O作OH⊥AD(或其延长线),垂足为H,设∠OAD=θ(0<θ<$\frac{π}{4}$),把OH,DH分别用含有θ的三角函数值表示,利用勾股定理求OD,再由辅助角公式求得最小值,则铺设的4条线路OA,OB,OC,OD总长度的最小值可求.
解答 解:(1)连接AB,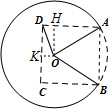
∵AB=10,∴正方形ABCD的面积为100,
又OA=OB=10,∴△AOB为正三角形,则$∠AOB=\frac{π}{3}$,
而圆的面积为100π,∴扇形AOB得面积为$\frac{100π}{6}=\frac{50π}{3}$,
又三角形AOB的面积为$\frac{1}{2}×10×5\sqrt{3}=25\sqrt{3}$.
∴弓形面积为$\frac{50π}{3}-25\sqrt{3}$,
则广场面积为100+$\frac{50π}{3}-25\sqrt{3}$(平方米);
(2)过O作OK⊥CD,垂足为K,过O作OH⊥AD(或其延长线),垂足为H,
设∠OAD=θ(0<θ<$\frac{π}{4}$),
则OH=10sinθ,AH=10cosθ,
∴DH=|AD-AH|=|2OH-AH|=|20sinθ-10cosθ|,
∴OD=$\sqrt{100si{n}^{2}θ+(20sinθ-10cosθ)^{2}}$=$\sqrt{300-200\sqrt{2}sin(2θ+\frac{π}{4})}$.
∴当θ=$\frac{π}{8}$时,$O{D}_{min}=10(\sqrt{2}-1)$.
∴铺设的4条线路OA,OB,OC,OD总长度的最小值为$20\sqrt{2}$(米).
点评 本题是应用题,考查简单的数学建模思想方法,考查圆在实际问题中的应用,训练了三角函数最值的求法,是中档题.

| A. | [-2$\sqrt{5}$,-4] | B. | (-2$\sqrt{5}$,-4] | C. | [-2$\sqrt{5}$,-4) | D. | (-2$\sqrt{5}$,-4) |
| 学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学偏差x | 20 | 15 | 13 | 3 | 2 | -5 | -10 | -18 |
| 物理偏差y | 6.5 | 3.5 | 3.5 | 1.5 | 0.5 | -0.5 | -2.5 | -3.5 |
(2)若这次考试该班数学平均分为118分,物理平均分为90.5,试预测数学成绩126分的同学的物理成绩.
参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\stackrel{∧}{y}$-$\stackrel{∧}{b}$x,
参考数据:$\sum_{i=1}^8{{x_i}{y_i}}$=324,$\sum_{i=1}^8{x_i^2}$=1256.
| A. | 表示直线 | B. | 表示线段 | C. | 表示圆 | D. | 表示半个圆 |
| A. | $({\frac{{\sqrt{3}}}{3},\frac{{4\sqrt{3}}}{11}}]$ | B. | $({\frac{{\sqrt{3}}}{9},\frac{{\sqrt{3}}}{3}})$ | C. | $({\frac{{\sqrt{3}}}{9},\frac{{4\sqrt{3}}}{11}}]$ | D. | $({\frac{{\sqrt{3}}}{9},\frac{{2\sqrt{3}}}{11}}]$ |
| A. | -84 | B. | 84 | C. | -36 | D. | 36 |
| A. | ?λ>0,使得$\overrightarrow c⊥\overrightarrow d$ | B. | ?λ>0,使得<$\overrightarrow{c}$,$\overrightarrow{d}$>=60° | ||
| C. | ?λ<0,使得<$\overrightarrow{c}$,$\overrightarrow{d}$>=30° | D. | ?λ>0,使得$\overrightarrow c=m\overrightarrow d(m$为不为0的常数) |