��Ŀ����
4����֪����$\overrightarrow a=��1��0����\overrightarrow b=��0��1����\overrightarrow c=\overrightarrow a+��\overrightarrow b���ˡ�R��$������$\overrightarrow d$��ͼ��ʾ��������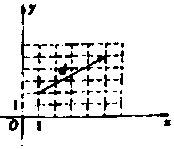
| A�� | ?�ˣ�0��ʹ��$\overrightarrow c��\overrightarrow d$ | B�� | ?�ˣ�0��ʹ�ã�$\overrightarrow{c}$��$\overrightarrow{d}$��=60�� | ||
| C�� | ?�ˣ�0��ʹ�ã�$\overrightarrow{c}$��$\overrightarrow{d}$��=30�� | D�� | ?�ˣ�0��ʹ��$\overrightarrow c=m\overrightarrow d��m$Ϊ��Ϊ0�ij����� |
���� ������ɵ�����$\overrightarrow{c}=\overrightarrow{a}+��\overrightarrow{b}=��1���ˣ�$������ͼ�ɵ�$\overrightarrow{d}$=��5��5��-��1��2��=��4��3�����ٶ�ѡ����һ�ж����ɣ�
��� �⣺����$\overrightarrow{c}=\overrightarrow{a}+��\overrightarrow{b}=��1���ˣ�$������ͼ�ɵ�$\overrightarrow{d}$=��5��5��-��1��2��=��4��3����
����A����$\overrightarrow c��\overrightarrow d$����1���ˣ�•��4��3��=0�����$��=-\frac{4}{3}��0$���ʴ���
����B������$\overrightarrow{c}$��$\overrightarrow{d}$��=60�㣬��$\frac{4+3��}{5\sqrt{1+{��}^{2}}}=\frac{1}{2}$����11��2+96��+39=0�������⣬�ʴ���
����C������$\overrightarrow{c}$��$\overrightarrow{d}$��=30�㣬��$\frac{4+3��}{5\sqrt{1+{��}^{2}}}=\frac{\sqrt{3}}{2}$����39��2-96��+11=0�������⣬�ʴ���
����D����$\overrightarrow c=m\overrightarrow d��m$Ϊ��Ϊ0�ij���������1���ˣ�=c��4��3������æ�=$\frac{3}{4}��0$������ȷ��
��ѡ��D
���� ���⿼���������������������ʡ��������߶���������������������������������ڻ����⣮

 53���ò�ϵ�д�
53���ò�ϵ�д�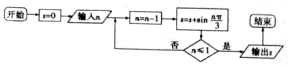
| A�� | $\frac{{\sqrt{3}}}{2}$ | B�� | $\sqrt{3}$ | C�� | $-\frac{{\sqrt{3}}}{2}$ | D�� | 0 |
| A�� | x1+x2-1��0 | B�� | x1+x2-1��0 | C�� | x2-x1��0 | D�� | x2-x1��0 |
| A�� | ��0��1�� | B�� | ��-�ޣ�1�� | C�� | ��0��+�ޣ� | D�� | $��-�ޣ�\frac{1}{2}��$ |
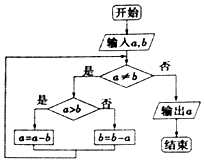
| A�� | 1 | B�� | 2 | C�� | 4 | D�� | 12 |
 ��ͼ��ԲO��һ�뾶Ϊ10��Բ�β�ƺ��Ϊ�������ܱ��������㳡�����Ҫ���ֹ滮�ڲ�ƺ�Ͻ�һ���㳡���㳡��״��ͼ�����߲�����ʾ�������ı��Σ�����A��B�����ڡ�O�ϣ�A��B��C��Dǡ��һ�������ε��ĸ����㣮���ݹ滮Ҫ����A��B��C��D�ĵ㴦��װ��յ�����豸����Բ��O��������ڵ�������4����A��B��C��D�ĵ���·OA��OB��OC��OD��
��ͼ��ԲO��һ�뾶Ϊ10��Բ�β�ƺ��Ϊ�������ܱ��������㳡�����Ҫ���ֹ滮�ڲ�ƺ�Ͻ�һ���㳡���㳡��״��ͼ�����߲�����ʾ�������ı��Σ�����A��B�����ڡ�O�ϣ�A��B��C��Dǡ��һ�������ε��ĸ����㣮���ݹ滮Ҫ����A��B��C��D�ĵ㴦��װ��յ�����豸����Բ��O��������ڵ�������4����A��B��C��D�ĵ���·OA��OB��OC��OD��