题目内容
已知函数f(x)=
+
,若x,y满足f(x+1)-f(y)>0,则x2+y2-2x+1的取值范围( )
| 1-x |
| 1+x |
| A、(1,10) | ||||
| B、[2,10] | ||||
C、(
| ||||
D、[
|
考点:简单线性规划,基本不等式,圆的一般方程
专题:不等式的解法及应用
分析:求函数的定义域,判断函数的奇偶性和单调性,将不等式转化为不等式组,利用线性规划的知识进行求解.
解答:
 解:由
解:由
,得
,即-1≤x≤1,
故函数的定义域为[-1,1],
f(-x)=
+
=f(x),
则函数f(x)是偶函数,
当0≤x≤1时,函数的导数f′(x)=-
+
=
<0,
即此时函数单调递减,
则f(x+1)-f(y)>0等价为f(x+1)>f(y),
即f(|x+1|)>f(|y|),
即
,
即
,
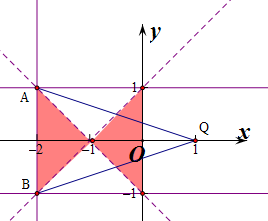
作出不等式组对应的平面区域如图:
x2+y2-2x+1=(x-1)2+y2的几何意义是区域内的点到点Q(1,0)的距离的平方,
由图象可知,OQ的距离最小为1,AQ或BQ的距离最大,此时最大值为(-2-1)2+12=10,
故x2+y2-2x+1的取值范围是(1,10),
故选:A
 解:由
解:由
|
|
故函数的定义域为[-1,1],
f(-x)=
| 1-x |
| 1+x |
则函数f(x)是偶函数,
当0≤x≤1时,函数的导数f′(x)=-
| 1 | ||
|
| 1 | ||
|
| ||||
|
即此时函数单调递减,
则f(x+1)-f(y)>0等价为f(x+1)>f(y),
即f(|x+1|)>f(|y|),
即
|
即
|
作出不等式组对应的平面区域如图:
x2+y2-2x+1=(x-1)2+y2的几何意义是区域内的点到点Q(1,0)的距离的平方,
由图象可知,OQ的距离最小为1,AQ或BQ的距离最大,此时最大值为(-2-1)2+12=10,
故x2+y2-2x+1的取值范围是(1,10),
故选:A
点评:本题主要考查线性规划的应用以及两点间的距离公式,利用数形结合是解决本题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
用三段论推理:“指数函数y=ax是增函数,因为y=(
)x是指数函数,所以y=(
)x是增函数”,你认为这个推理( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、大前提错误 |
| B、小前提错误 |
| C、推理形式错误 |
| D、是正确的 |
设数列{an}满足a1=a2=1,a3=2,且对任意正整数n,都有anan+1an+2≠1,又anan+1an+2an+3=an+an+1+an+2+an+3,则a1+a2+…+a100的值为( )
| A、200 | B、180 |
| C、160 | D、100 |
定义在R上的奇函数y=f(x)满足不等式:
>0(x1≠x2),若当a>0时,f(a2)+f(b2-1)<0,则
的取值范围是( )
| f(x2)-f(x1) |
| x2-x1 |
| (a+1)2+b2 |
| A、(0,2) | ||
| B、(1,2) | ||
C、(0,
| ||
D、(1,
|
函数f(x)=lnx-x的单调减区间为( )
| A、(-∞,0),(1,+∞) |
| B、(1,+∞) |
| C、(-∞,0) |
| D、(0,1) |