题目内容
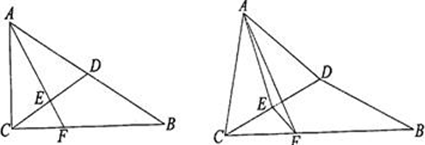
已知D、E、F分别为△ABC的三边BC、AC、AB的中点,求证:
+
+
=
.
| AD |
| BE |
| CF |
| 0 |
考点:向量的三角形法则
专题:平面向量及应用
分析:根据向量的三角形法则证明.
解答:
证明:因为D、E、F分别为△ABC的三边BC、AC、AB的中点,
所以
=
(
+
),
=
(
+
),
=
(
+
),
三式相加得
+
+
=
(
+
+
+
+
+
)=
.
所以
| AD |
| 1 |
| 2 |
| AB |
| AC |
| BE |
| 1 |
| 2 |
| BA |
| BC |
| CF |
| 1 |
| 2 |
| CB |
| CA |
三式相加得
| AD |
| BE |
| CF |
| 1 |
| 2 |
| AB |
| AC |
| BA |
| BC |
| CB |
| CA |
| 0 |
点评:本题考查了三角形中线的性质以及相反向量的和为
.
| 0 |

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
执行以下程序框图,所得的结果为( )
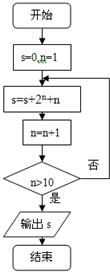

| A、1067 | B、2100 |
| C、2101 | D、4160 |
已知函数f(x)=
+
,若x,y满足f(x+1)-f(y)>0,则x2+y2-2x+1的取值范围( )
| 1-x |
| 1+x |
| A、(1,10) | ||||
| B、[2,10] | ||||
C、(
| ||||
D、[
|
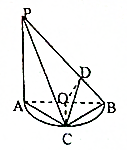 如图,PA垂直⊙O所在平面ABC,AB为⊙O的直径,PA=AB,BD=
如图,PA垂直⊙O所在平面ABC,AB为⊙O的直径,PA=AB,BD=