题目内容
用三段论推理:“指数函数y=ax是增函数,因为y=(
)x是指数函数,所以y=(
)x是增函数”,你认为这个推理( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、大前提错误 |
| B、小前提错误 |
| C、推理形式错误 |
| D、是正确的 |
考点:演绎推理的基本方法
专题:综合题,推理和证明
分析:指数函数y=ax(a>0且a≠1)是R上的增函数,这个说法是错误的,要根据所给的底数的取值不同分类说出函数的不同的单调性,即大前提是错误的.
解答:
解:指数函数y=ax(a>0且a≠1)是R上的增函数,
这个说法是错误的,要根据所给的底数的取值不同分类说出函数的不同的单调性,
大前提是错误的,
∴得到的结论是错误的,
∴在以上三段论推理中,大前提错误.
故选A.
这个说法是错误的,要根据所给的底数的取值不同分类说出函数的不同的单调性,
大前提是错误的,
∴得到的结论是错误的,
∴在以上三段论推理中,大前提错误.
故选A.
点评:本题考查演绎推理的基本方法,解题的关键是理解演绎推理的三段论原理,在大前提和小前提中,若有一个说法是错误的,则得到的结论就是错误的.

练习册系列答案
相关题目
把下面在平面内成立的结论:
(1)如果一条直线与两条平行线中的一条相交,则它与另一条相交
(2)如果两条直线同时与第三条直线平行,则这两条直线平行
(3)如果一条直线与两条平行线中的一条垂直,则它与另一条垂直
(4)如果两条直线同时与第三条直线垂直,则这两条直线平行
类比地推广到空间,且结论也正确的是( )
(1)如果一条直线与两条平行线中的一条相交,则它与另一条相交
(2)如果两条直线同时与第三条直线平行,则这两条直线平行
(3)如果一条直线与两条平行线中的一条垂直,则它与另一条垂直
(4)如果两条直线同时与第三条直线垂直,则这两条直线平行
类比地推广到空间,且结论也正确的是( )
| A、(1)(2) |
| B、(2)(3) |
| C、(2)(4) |
| D、(3)(4) |
已知函数f(x)=
+
,若x,y满足f(x+1)-f(y)>0,则x2+y2-2x+1的取值范围( )
| 1-x |
| 1+x |
| A、(1,10) | ||||
| B、[2,10] | ||||
C、(
| ||||
D、[
|
抛物线y2=12x被直线x-y-3=0截得弦长的值为( )
| A、21 | B、16 | C、24 | D、30 |
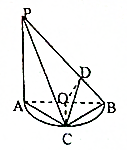 如图,PA垂直⊙O所在平面ABC,AB为⊙O的直径,PA=AB,BD=
如图,PA垂直⊙O所在平面ABC,AB为⊙O的直径,PA=AB,BD=