题目内容
定义在R上的奇函数y=f(x)满足不等式:
>0(x1≠x2),若当a>0时,f(a2)+f(b2-1)<0,则
的取值范围是( )
| f(x2)-f(x1) |
| x2-x1 |
| (a+1)2+b2 |
| A、(0,2) | ||
| B、(1,2) | ||
C、(0,
| ||
D、(1,
|
考点:两点间距离公式的应用,函数单调性的性质
专题:计算题,函数的性质及应用
分析:先y=f(x)满足不等式:
>0(x1≠x2),得函数f(x)是定义在R上的增函数;再利用函数f(x)是定义在R上的奇函数得f(-x)=-f(x),由当a>0时,f(a2)+f(b2-1)<0,可得a2+b2<1,表示以原点为圆心,1为半径的圆内部分,根据
的几何意义是(a,b)与(-1,0)的距离,即可得出结论.
| f(x2)-f(x1) |
| x2-x1 |
| (a+1)2+b2 |
解答:
解:由y=f(x)满足不等式:
>0(x1≠x2),得函数f(x)是定义在R上的增函数
又因为函数f(x)是定义在R上的奇函数,所以有函数f(-x)=-f(x)
因为当a>0时,f(a2)+f(b2-1)<0,
所以a2+b2<1,表示以原点为圆心,1为半径的圆内部分,
因为
的几何意义是(a,b)与(-1,0)的距离,
所以
的取值范围是(0,2),
故选:A.
| f(x2)-f(x1) |
| x2-x1 |
又因为函数f(x)是定义在R上的奇函数,所以有函数f(-x)=-f(x)
因为当a>0时,f(a2)+f(b2-1)<0,
所以a2+b2<1,表示以原点为圆心,1为半径的圆内部分,
因为
| (a+1)2+b2 |
所以
| (a+1)2+b2 |
故选:A.
点评:本题主要考查函数奇偶性和单调性的综合应用问题.关键点有两处:①判断出函数f(x)的单调性;②利用奇函数的性质得到函数f(-x)=-f(x)③明确目标函数的几何意义.

练习册系列答案
相关题目
已知函数f(x)=
+
,若x,y满足f(x+1)-f(y)>0,则x2+y2-2x+1的取值范围( )
| 1-x |
| 1+x |
| A、(1,10) | ||||
| B、[2,10] | ||||
C、(
| ||||
D、[
|
抛物线y2=12x被直线x-y-3=0截得弦长的值为( )
| A、21 | B、16 | C、24 | D、30 |
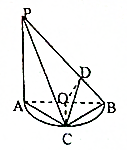 如图,PA垂直⊙O所在平面ABC,AB为⊙O的直径,PA=AB,BD=
如图,PA垂直⊙O所在平面ABC,AB为⊙O的直径,PA=AB,BD=