题目内容
若直线l不平行于平面a，且l?a，则（ ）
| A、a内所有直线与l异面 |
| B、a内不存在与l平行的直线 |
| C、a内存在唯一的直线与l平行 |
| D、a内的直线与l都相交 |
考点：直线与平面平行的判定
专题：空间位置关系与距离
分析：a内与l相交的直线在同一面内，推断出A选项错误．
直线l与面相交的点，过此点的所有直线均与l相交，平面内其他的线则不与其相交，推断出C，D项说法错误．
利用反证法和线面平行的判定定理推断出B项正确．
直线l与面相交的点，过此点的所有直线均与l相交，平面内其他的线则不与其相交，推断出C，D项说法错误．
利用反证法和线面平行的判定定理推断出B项正确．
解答：
解：a内与l相交的直线在同一面内，故A选项错误．
直线l与面相交的点，过此点的所有直线均与l相交，平面内其他的线则不与其相交，故C，D项说法错误．
若a内存在与l平行的直线，则根据线面平行的判定定理可知l与面a平行，已知直线l不平行于平面a，故a内不存在与l平行的直线，B项说法正确．
故选B．
直线l与面相交的点，过此点的所有直线均与l相交，平面内其他的线则不与其相交，故C，D项说法错误．
若a内存在与l平行的直线，则根据线面平行的判定定理可知l与面a平行，已知直线l不平行于平面a，故a内不存在与l平行的直线，B项说法正确．
故选B．
点评：本题主要考查了直线与平面的位置关系，线面平行判定定理的运用．考查了学生逻辑推理能力．
练习册系列答案
相关题目
若某空间几何体的三视图如图所示，则该几何体的表面积是（ ）
A、2+
| ||||||
B、2（1+
| ||||||
C、
| ||||||
D、2+
|
点F（c，0）为双曲线
-
=1（a＞0，b＞0）的右焦点，点P在双曲线上，线段PF与圆（x-
）2+y2=
相切于点Q，且
=2
，则双曲线的离心率等于（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| c |
| 3 |
| b2 |
| 9 |
| PQ |
| QF |
A、
| ||
B、
| ||
C、
| ||
| D、2 |
关于以下四个命题，不正确的是（ ）
①若函数y=2x的定义域是{x|x≤0}，则它的值域为{y|y≤1}
②若函数y=
的定义域是{x|x＞2}，则它的值域为{y|y＜
}
③若函数y=x2的值域是{y|0≤y≤4}，则它的定义域一定是{x|-2≤x≤2}
④若函数y=log2x的值域是{y|y≤3}，则它的定义域是{x|0＜x≤8}．
①若函数y=2x的定义域是{x|x≤0}，则它的值域为{y|y≤1}
②若函数y=
| 1 |
| x |
| 1 |
| 2 |
③若函数y=x2的值域是{y|0≤y≤4}，则它的定义域一定是{x|-2≤x≤2}
④若函数y=log2x的值域是{y|y≤3}，则它的定义域是{x|0＜x≤8}．
| A、①②③ | B、②③④ |
| C、①③④ | D、①②④ |
《张丘建算经》卷上第22题为：今有女善织，日益功疾，且从第2天起，每天比前一天多织相同量的布，若第1天织5尺布，现在一月（按30天计）共织390尺布，则每天比前一天多织（ ）尺布．（不作近似计算）
A、
| ||
B、
| ||
C、
| ||
D、
|
圆x2+y2+2kx+k2-1=0与圆x2+y2+2（k+1）y+k2+2k=0的圆心之间的最短距离是（ ）
A、
| ||||
B、2
| ||||
| C、1 | ||||
D、
|
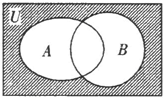设全集U={1，2，3，4，5，6，7，8}，集合A={2，4，5，7}，B={1，4，7，8}，那么如图所示的阴影部分所表示的集合是（ ）| A、{3，6} |
| B、{4，7} |
| C、{1，2，4，5，7，8} |
| D、{1，2，3，5，6，8} |