题目内容
点F(c,0)为双曲线
-
=1(a>0,b>0)的右焦点,点P在双曲线上,线段PF与圆(x-
)2+y2=
相切于点Q,且
=2
,则双曲线的离心率等于( )
| x2 |
| a2 |
| y2 |
| b2 |
| c |
| 3 |
| b2 |
| 9 |
| PQ |
| QF |
A、
| ||
B、
| ||
C、
| ||
| D、2 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:设椭圆的左焦点为F1,确定PF1⊥PF,|PF1|=b,|PF|=2a+b,即可求得椭圆的离心率.
解答:
解:设双曲线的左焦点为F1,连接F1,设圆心为C,则
∵(x-
)2+y2=
,
∴圆心坐标为(
,0),半径为r=
∴|F1F|=3|FC|
∵
=2
,
∴PF1∥QC,|PF1|=b
∴|PF|=2a-b
∵线段PF与圆(x-
)2+y2=
(其中c2=a2+b2)相切于点Q,
∴CQ⊥PF
∴PF1⊥PF
∴b2+(2a+b)2=4c2
∴b2+(2a+b)2=4(a2+b2)
∴b=2a,
∴c=
a
∴e=
=
故选:C.
∵(x-
| c |
| 3 |
| b2 |
| 9 |
∴圆心坐标为(
| c |
| 3 |
| b |
| 3 |
∴|F1F|=3|FC|
∵
| PQ |
| QF |
∴PF1∥QC,|PF1|=b
∴|PF|=2a-b
∵线段PF与圆(x-
| c |
| 3 |
| b2 |
| 9 |
∴CQ⊥PF
∴PF1⊥PF
∴b2+(2a+b)2=4c2
∴b2+(2a+b)2=4(a2+b2)
∴b=2a,
∴c=
| 5 |
∴e=
| c |
| a |
| 5 |
故选:C.
点评:本题考查双曲线的几何性质,考查直线与圆的位置关系,确定几何量的关系是关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
定义在R上的函数f(x)满足f(x+6)=f(x),当-3≤x<-1时,f(x)=-(x+2)2;当-1≤x<3时,f(x)=x.则f(1)+f(2)+f(3)+…+f(2013)等于( )
| A、335 | B、337 |
| C、1678 | D、2012 |
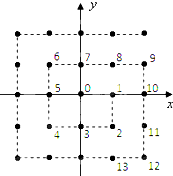 如图,将平面直角坐标系的格点(横、纵坐标均为整数的点)按如下规则标上数字标签:原点处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)标5,点(-1,1)处标6,点(0,1)处标7,以此类推,则标签2013×2014的格点的坐标为( )
如图,将平面直角坐标系的格点(横、纵坐标均为整数的点)按如下规则标上数字标签:原点处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)标5,点(-1,1)处标6,点(0,1)处标7,以此类推,则标签2013×2014的格点的坐标为( )| A、(-1007,1007) |
| B、(1007,1006) |
| C、(-1007,-1007) |
| D、(1006,-1007) |
市场上供应的灯泡中,甲厂产品占70%,乙厂占30%,甲厂产品的合格率是95%,乙厂的合格率是80%,则从市场上买到一个是甲厂生产的合格灯泡的概率是( )
| A、0.665 | B、0.56 |
| C、0.24 | D、0.285 |
下列式子正确的是( )
A、
| ||
B、
| ||
C、
| ||
D、(
|
若直线l不平行于平面a,且l?a,则( )
| A、a内所有直线与l异面 |
| B、a内不存在与l平行的直线 |
| C、a内存在唯一的直线与l平行 |
| D、a内的直线与l都相交 |
若x>1时,不等式x+
≥a恒成立,则实数a的最大值为( )
| 1 |
| x-1 |
| A、2 | B、3 | C、4 | D、5 |
若正多边形有n条边,它们对应的向量依次为
,
,…,
,则这n个向量( )
| a1 |
| a2 |
| an |
| A、都相等 | B、都共线 |
| C、都不共线 | D、模都相等 |