题目内容
若某空间几何体的三视图如图所示，则该几何体的表面积是（ ）
A、2+
| ||||||
B、2（1+
| ||||||
C、
| ||||||
D、2+
|
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知中的三视图可得，该几何体是一个以侧视图为底面的三棱柱，求出底面面积，周长和棱柱的高，可得几何体的表面积．
解答：
解：由已知中的三视图可得，该几何体是一个以侧视图为底面的三棱柱，
底面的两直角边长分别为1和
，故斜率长
=
，
故底面面积：S底=
，
底面周长：C=1+
+
，
又由棱柱的高h=
，
故棱柱的侧面积S侧=Ch=（1+
+
）×
=
+2+
，
故该几何体的表面积S=2×S底+S侧=
+
+2+
=2（1+
）+
，
故选：B
底面的两直角边长分别为1和
| 2 |
12+
|
| 3 |
故底面面积：S底=
| ||
| 2 |
底面周长：C=1+
| 2 |
| 3 |
又由棱柱的高h=
| 2 |
故棱柱的侧面积S侧=Ch=（1+
| 2 |
| 3 |
| 2 |
| 2 |
| 6 |
故该几何体的表面积S=2×S底+S侧=
| 2 |
| 2 |
| 6 |
| 2 |
| 6 |
故选：B
点评：本题考查的知识点是由三视图求体积，其中根据已知的三视图分析出几何体的形状是解答的关键．
练习册系列答案
相关题目
定义在R上的函数f（x）满足f（x+6）=f（x），当-3≤x＜-1时，f（x）=-（x+2）2；当-1≤x＜3时，f（x）=x．则f（1）+f（2）+f（3）+…+f（2013）等于（ ）
| A、335 | B、337 |
| C、1678 | D、2012 |
函数y=
的定义域是（ ）
log
|
| A、[1，+∞） | ||
B、（
| ||
| C、（1，+∞） | ||
D、（
|
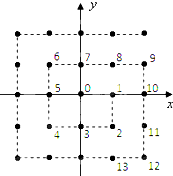如图，将平面直角坐标系的格点（横、纵坐标均为整数的点）按如下规则标上数字标签：原点处标0，点（1，0）处标1，点（1，-1）处标2，点（0，-1）处标3，点（-1，-1）处标4，点（-1，0）标5，点（-1，1）处标6，点（0，1）处标7，以此类推，则标签2013×2014的格点的坐标为（ ）| A、（-1007，1007） |
| B、（1007，1006） |
| C、（-1007，-1007） |
| D、（1006，-1007） |
市场上供应的灯泡中，甲厂产品占70%，乙厂占30%，甲厂产品的合格率是95%，乙厂的合格率是80%，则从市场上买到一个是甲厂生产的合格灯泡的概率是（ ）
| A、0.665 | B、0.56 |
| C、0.24 | D、0.285 |
若直线l不平行于平面a，且l?a，则（ ）
| A、a内所有直线与l异面 |
| B、a内不存在与l平行的直线 |
| C、a内存在唯一的直线与l平行 |
| D、a内的直线与l都相交 |
数列{an}的通项公式为an=
，其前n项和为Sn，则S10的值为（ ）
| 1 |
| n2+n |
A、
| ||
B、
| ||
C、
| ||
D、
|