题目内容
16.在△ABC中,已知BC=1,B=$\frac{π}{3}$,△ABC的面积为$\sqrt{3}$,则AC的长为( )| A. | 3 | B. | $\sqrt{13}$ | C. | $\sqrt{21}$ | D. | $\sqrt{57}$ |
分析 由已知利用三角形面积公式可求AB的值,进而利用余弦定理可求AC的值.
解答 解:∵BC=1,B=$\frac{π}{3}$,
△ABC的面积为$\sqrt{3}$=$\frac{1}{2}$BC•AB•sinB=$\frac{1}{2}×AB×1×\frac{\sqrt{3}}{2}$,
∴AB=4,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}-2AB•BC•cosB}$=$\sqrt{16+1-2×4×1×\frac{1}{2}}$=$\sqrt{13}$.
故选:B.
点评 本题主要考查了三角形面积公式,余弦定理在解三角形中的应用,属于基础题.

练习册系列答案
相关题目
4.三棱锥P-ABC的四个顶点均在半径为5的球面上,且△ABC是斜边长为8的等腰直角三角形,则三棱锥P-ABC的体积的最大值为( )
| A. | 64 | B. | 128 | C. | $\frac{64}{3}$ | D. | $\frac{128}{3}$ |
11.若数列{an},{bn}的通项公式分别为an=(-1)n+2016•a,bn=2+$\frac{{{{(-1)}^{n+2017}}}}{n}$,且an<bn,对任意n∈N*恒成立,则实数a的取值范围是( )
| A. | $[-1,\frac{1}{2})$ | B. | [-1,1) | C. | [-2,1) | D. | $[-2,\frac{3}{2})$ |
1.对任意的x>0,总有f(x)=a-x-|lgx|≤0,则a的取值范围是( )
| A. | (-∞,lge-lg(lge)] | B. | (-∞,1] | C. | [1,lge-lg(lge)] | D. | [lge-lg(lge),+∞) |
8.执行如图所示的程序框图,如果输入n=3,则输出的S值为( )
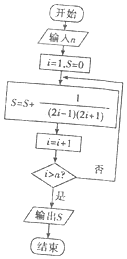

| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{7}$ | D. | $\frac{6}{7}$ |
10.一个几何体的三视图及尺寸如图所示,则该几何体的体积为( )


| A. | 24 | B. | 30 | C. | 48 | D. | 72 |
11.已知$\overrightarrow a,\overrightarrow b$均为单位向量,它们的夹角为60°,那么$|{3\overrightarrow a+\overrightarrow b}|$等于( )
| A. | 4 | B. | $\sqrt{13}$ | C. | $\sqrt{10}$ | D. | $\sqrt{7}$ |