题目内容
6.若$\int_0^{\frac{π}{4}}{cosxdx=\int_0^a{{x^2}dx}}$,则a3=$\frac{3\sqrt{2}}{2}$.分析 首先等式两边分别求定积分,得到关于a 的方程解之.
解答 解:由题可知$\int_0^{\frac{π}{4}}{cosxdx=\int_0^a{{x^2}dx}}$,
得到sinx|${\;}_{0}^{\frac{π}{4}}$=$\frac{1}{3}{x}^{3}{|}_{0}^{a}$,∴$\frac{1}{3}{a}^{3}=\frac{\sqrt{2}}{2}$,即${a}^{3}=\frac{3\sqrt{2}}{2}$.
故答案为:$\frac{3\sqrt{2}}{2}$.
点评 本题考查了定积分的计算;熟练掌握基本初等函数的求导公式是关键,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.平面内给定三个向量$\overrightarrow{a}$=(3,2),$\overrightarrow{b}$=(-1,2),$\overrightarrow{c}$=(4,1),若($\overrightarrow{a}$+k$\overrightarrow{c}$)∥(2$\overrightarrow{b}$-$\overrightarrow{a}$)则实数k的值为( )
| A. | $\frac{16}{13}$ | B. | $\frac{3}{4}$ | C. | $-\frac{16}{13}$ | D. | $-\frac{4}{3}$ |
15.(文)已知定义在实数集R上的函数f(x)满足f(2)=7,且f(x)的导数f′(x)在R上恒有f′(x)<3(x∈R),则不等式f(x)<3x+1的解集为( )
| A. | (1,+∞) | B. | (-∞,-2) | C. | (-∞.-1)∪(1,+∞) | D. | (2,+∞) |
16.在△ABC中,已知BC=1,B=$\frac{π}{3}$,△ABC的面积为$\sqrt{3}$,则AC的长为( )
| A. | 3 | B. | $\sqrt{13}$ | C. | $\sqrt{21}$ | D. | $\sqrt{57}$ |
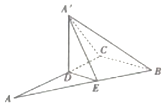 如图,将直角△ABC沿着平行BC边的直线DE折起,使得平面A′DE⊥平面BCDE,其中D、E分别在AC、AB边上,且AC⊥BC,BC=3,AB=5,点A′为点A折后对应的点,当四棱锥A′-BCDE的体积取得最大值时,求AD的长.
如图,将直角△ABC沿着平行BC边的直线DE折起,使得平面A′DE⊥平面BCDE,其中D、E分别在AC、AB边上,且AC⊥BC,BC=3,AB=5,点A′为点A折后对应的点,当四棱锥A′-BCDE的体积取得最大值时,求AD的长.