题目内容
11.已知$\overrightarrow a,\overrightarrow b$均为单位向量,它们的夹角为60°,那么$|{3\overrightarrow a+\overrightarrow b}|$等于( )| A. | 4 | B. | $\sqrt{13}$ | C. | $\sqrt{10}$ | D. | $\sqrt{7}$ |
分析 根据平面向量的数量积,计算模长$|{3\overrightarrow a+\overrightarrow b}|$即可.
解答 解:$\overrightarrow a,\overrightarrow b$均为单位向量,它们的夹角为60°,
∴$\overrightarrow{a}$$•\overrightarrow{b}$=1×1×cos60°=$\frac{1}{2}$,
∴${(3\overrightarrow{a}+\overrightarrow{b})}^{2}$=9${\overrightarrow{a}}^{2}$+6$\overrightarrow{a}$$•\overrightarrow{b}$+${\overrightarrow{b}}^{2}$=9+6×$\frac{1}{2}$+1=13,
∴$|{3\overrightarrow a+\overrightarrow b}|$=$\sqrt{13}$.
故选:B.
点评 本题考查了利用平面向量的数量积求模长的应用问题,是基础题.

练习册系列答案
相关题目
16.在△ABC中,已知BC=1,B=$\frac{π}{3}$,△ABC的面积为$\sqrt{3}$,则AC的长为( )
| A. | 3 | B. | $\sqrt{13}$ | C. | $\sqrt{21}$ | D. | $\sqrt{57}$ |
2.设α、β、γ为平面,m、n、l为直线,则能推m⊥β是( )
| A. | α⊥β,α∩β=l,m⊥l | B. | α∩γ=m,α⊥γ,β⊥γ | C. | α⊥γ,β⊥γ,m⊥α | D. | n⊥α,n⊥β,m⊥α |
16.某中学将100名高二文科生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A,B两种不同的教学方式分别在甲、乙两个班进行教改实验.为了了解教学效果,期末考试后,陈老师对甲、乙两个班级的学生成绩进行统计分析,画出频率分布直方图(如图).记成绩不低于90分者为“成绩优秀”.
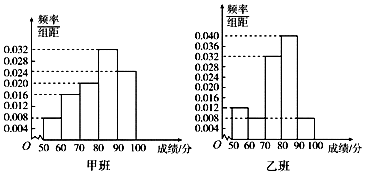
(Ⅰ)根据频率分布直方图填写下面2×2列联表;
(Ⅱ)判断能否在犯错误的概率不超过0.05的前提下认为:“成绩优秀”与教学方式有关?
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$.

(Ⅰ)根据频率分布直方图填写下面2×2列联表;
| 甲班(A方式) | 乙班(B方式) | 总计 | |
| 成绩优秀 | 12 | 4 | 20 |
| 成绩不优秀 | 38 | 46 | 80 |
| 总计 | 50 | 50 | 100 |
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$.
| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
3.为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下列表:
已知在全部50人中随机抽取1人,抽到喜爱打篮球的学生的概率为$\frac{3}{5}$.
(1)请将上表补充完整(不用写计算过程);
(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理由;下面的临界值表供参考:
(参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
(1)请将上表补充完整(不用写计算过程);
(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理由;下面的临界值表供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
20.已知函数$y=|{sin({2x-\frac{π}{6}})}|$,以下说法正确的是( )
| A. | 函数的最小正周期为$\frac{π}{4}$ | B. | 函数是偶函数 | ||
| C. | 函数图象的一条对称轴为$x=\frac{π}{3}$ | D. | 函数在$[{\frac{2π}{3},\frac{5π}{6}}]$上为减函数 |
1.已知圆${(x-1)^2}+{y^2}=\frac{3}{4}$的一条切线y=kx与双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$没有公共点,则双曲线C的离心率的取值范围是( )
| A. | $(1,\sqrt{3})$ | B. | (1,2] | C. | $(\sqrt{3},+∞)$ | D. | [2,+∞) |
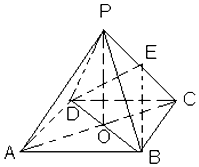 如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.求证:
如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.求证: