题目内容
设α、β、γ均为锐角,cosα2+cosβ2+cosγ2+2cosαcosβcosγ=1,求证:α+β+γ=π.
考点:三角函数恒等式的证明
专题:证明题,三角函数的求值
分析:令 x=cosα,y=cosβ,z=cosγ,则由已知可得一元二次方程f(z)=z2+2xyz+(x2+y2-1)=0,又 x,y,z>0,可解得z=-xy+
=cos(π-α-β),即 cos(π-α-β)=cosγ>0.又π-α-β 属于(0,π),即可解得:π-α-β=γ,从而得解α+β+γ=π,即可得证.
| (1-x2)(1-y2) |
解答:
证明:令 x=cosα,y=cosβ,z=cosγ,
则 x2+y2+z2+2xyz=1.(1)
又因为 α,β,γ 是锐角,
所以 x,y,z属于(0,1).
由(1)得:f(z)=z2+2xyz+(x2+y2-1)=0.
所以:△=4x2y2-4(x2+y2-1)=4 (1-x2)(1-y2).
又因为 1-x2>0,1-y2>0,
所以 z1=-xy+
,z2=-xy-
.
又因为 x,y,z>0,
所以 z=-xy+
=-cosα cosβ+sinα sinβ
=-cos(α+β)
=cos(π-α-β).
即 cos(π-α-β)=cosγ>0.
又因为 π-α-β 属于(0,π),
所以 π-α-β=γ.
即 α+β+γ=π.得证.
则 x2+y2+z2+2xyz=1.(1)
又因为 α,β,γ 是锐角,
所以 x,y,z属于(0,1).
由(1)得:f(z)=z2+2xyz+(x2+y2-1)=0.
所以:△=4x2y2-4(x2+y2-1)=4 (1-x2)(1-y2).
又因为 1-x2>0,1-y2>0,
所以 z1=-xy+
| (1-x2)(1-y2) |
| (1-x2)(1-y2) |
又因为 x,y,z>0,
所以 z=-xy+
| (1-x2)(1-y2) |
=-cosα cosβ+sinα sinβ
=-cos(α+β)
=cos(π-α-β).
即 cos(π-α-β)=cosγ>0.
又因为 π-α-β 属于(0,π),
所以 π-α-β=γ.
即 α+β+γ=π.得证.
点评:本题主要考查了一元二次方程的解法,考查了三角函数恒等式的证明,综合性强,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知命题①若a>b,则
<
,②若-2≤x≤0,则(x+2)(x-3)≤0,则下列说法正确的是( )
| 1 |
| a |
| 1 |
| b |
| A、①的逆命题为真 |
| B、②的逆命题为真 |
| C、①的逆否命题为真 |
| D、②的逆否命题为真 |
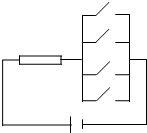 某种开关在电路中闭合的概率为p,现将4只这种开关并联在某电路中(如图所示),若该电路为通路的概率为
某种开关在电路中闭合的概率为p,现将4只这种开关并联在某电路中(如图所示),若该电路为通路的概率为| 65 |
| 81 |
A、
| ||
B、
| ||
C、
| ||
D、
|